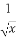题目内容
下列曲线的所有切线构成的集合中,存在无数对互相垂直的切线的曲线是( )
(A)f(x)=ex (B)f(x)=x3
(C)f(x)=lnx (D)f(x)=sinx
D
【解析】设切点的横坐标为x1,x2,
则存在无数对互相垂直的切线,即f'(x1)·f'(x2)=-1有无数对x1,x2使之成立,
对于A由于f'(x)=ex>0,
所以不存在f'(x1)·f'(x2)=-1成立;
对于B由于f'(x)=3x2≥0,
所以也不存在f'(x1)·f'(x2)=-1成立;
对于C由于f(x)=lnx的定义域为(0,+∞),
∴f'(x)=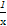 >0;
>0;
对于D,由于f'(x)=cosx,
所以f'(x1)·f'(x2)=cosx1·cosx2,
若x1=2mπ,m∈Z,x2=(2k+1)π,k∈Z,
则f'(x1)·f'(x2)=-1恒成立.

练习册系列答案
相关题目