题目内容
椭圆G：
的两个焦点
、
，M是椭圆上一点，且满足
．
（1）求离心率
的取值范围；
（2）当离心率取得最小值时，点
到椭圆上的点的最远距离为
；
①求此时椭圆G的方程；
②设斜率为
（
）的直线
与椭圆G相交于不同的两点A、B，Q为AB的中点，问：A、B两点能否关于过点
、Q的直线对称？若能，求出的取值范围；若不能，请说明理由．
解：（1）离心率的
的取值范围是
；
（2）①当离心率的取最小值
时，椭圆的方程可表示为
。
设
是椭圆上的一点，则
其中
。
若
，则当
时，
有最大值
所以
解得
（均舍去）。
若
，则当
时，有最大值
所以
解得
∴所求椭圆方程为
；
②设
，则由
两式相减得
……. ①
又直线
⊥直线
∴直线的方程为
，将
坐标代入得
……. ②
由①②解得
，而点Q必在椭圆得内部，∴
，由此可得
，又
∴
故当
时，A,B两点关于过点P,Q得直线对称.）
练习册系列答案
相关题目
的两个焦点F1（－c，0）、F2（c，0），M是椭圆上的一点，且满足
求此时椭圆G的方程；（ⅱ）设斜率为k（k≠0）的直线l与椭圆G相交于不同的两点A、B，Q为AB的中点，问A、B两点能否关于过点
的直线对称？若能，求出k的取值范围；若不能，请说明理由
的两个焦点为
是椭圆上一点，且满
．[来源:学#科#网]
的取值范围；
到椭圆上点的最远距离为
．
的直线
与椭圆G相交于不同两点
，
为
的中点，问：
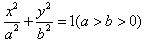的两个焦点为F1、F2，点P在椭圆G上，且PF1⊥F1F2，且
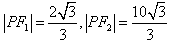，斜率为1的直线l与椭圆G交与A、B两点，以AB为底边作等腰三角形，顶点为P（-3，2），
的两个焦点为F1、F2，短轴两端点B1、B2，已知F1、F2、B1、B2四点共圆 ，且点N（0，3）到椭圆上的点的最远距离为
的直线对称？若能，求出k的取值范围；若不能，请说明理由。
的两个焦点为F1、F2，短轴两端点B1、B2，已知
）、Q的直线对称？若能，求出k的取值范围；若不能，请说明理由．