题目内容
在平面直角坐标系
中，若圆
上存在
，
两点关于点
成中心对称，则直线
的方程为 .
x+y=3
解析试题分析：由题意，圆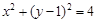
的圆心坐标为C（0，1），
∵圆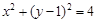上存在A，B两点关于点P（1，2）成中心对称，
∴CP⊥AB，P为AB的中点，
∵
，∴
，
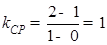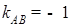∴直线AB的方程为y-2=-（x-1），即x+y-3=0．
考点：直线与圆的位置关系．
练习册系列答案
相关题目
题目内容
在平面直角坐标系中，若圆上存在，两点关于点成中心对称，则直线的方程为 .
x+y=3
解析试题分析：由题意，圆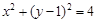的圆心坐标为C（0，1），
∵圆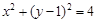上存在A，B两点关于点P（1，2）成中心对称，
∴CP⊥AB，P为AB的中点，
∵，∴，
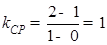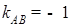∴直线AB的方程为y-2=-（x-1），即x+y-3=0．
考点：直线与圆的位置关系．
.设该圆过点（3，5）的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积为 
，点
在直线
上，若过点
与圆
交于
、
两点，且点
的中点，则点
的取值范围是 ．
：
与圆
：
的公共弦长等于.
中，已知点
在圆
内，动直线
过点
且交圆
于
两点，若△ABC的面积的最大值为
，则实数
的取值范围为 ．
，则直线l的斜率k的取值范围为________．