题目内容
20．如果一扇形的圆心角为120°，半径等于 10cm，则扇形的面积为\frac{100π}{3} cm2．分析 先求弧长，再求面积即可．
解答 解：扇形的弧长是l=\frac{2π}{3}×10=\frac{20π}{3}
则扇形的面积是：\frac{1}{2}lr=\frac{1}{2}×\frac{20π}{3}×10=\frac{100π}{3}cm2．
故答案为：\frac{100π}{3}．
点评 本题考查扇形弧长、面积公式，是基础题．
练习册系列答案
相关题目
4．已知定义在（-∞，-∞）的奇函数f（x）满足f（2-x）=f（x），当x∈（\frac{1}{2}，\frac{3}{2}），f（x）=x3+1nx，则f（2015）的值为（ ）
| A． | 1 | B． | -1 | C． | 0 | D． | 3 |
15．设全集U=R，A={x|0＜x＜2}，B={x|x＜1}，则图中阴影部分表示的集合为（ ）
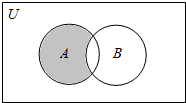
| A． | {x|x≥1} | B． | {x|0≤x≤1} | C． | {x|1≤x＜2} | D． | {x|x≤1} |
5．某单位有老年人30 人，中年人60人，青年人90人，为了调查他们的身体状况的某项指标，需从他们中间抽取一个容量为36样本，则老年人、中年人、青年人分别各抽取的人数是（ ）
| A． | 6，12，18 | B． | 7，11，19 | C． | 6，13，17 | D． | 7，12，17 |
12．球面上有A、B、C、D四个点，若AB、AC、AD两两垂直，且AB=AC=AD=4，则该球的表面积为（ ）
| A． | \frac{80π}{3} | B． | 32π | C． | 42π | D． | 48π |
9．
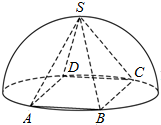底面是正多边形，顶点在底面的射影是底面中心的棱锥叫正棱锥．如图，半球内有一内接正四棱锥S-ABCD，该四棱锥的体积为\frac{4\sqrt{2}}{3}，则该半球的体积为．（ ）
底面是正多边形，顶点在底面的射影是底面中心的棱锥叫正棱锥．如图，半球内有一内接正四棱锥S-ABCD，该四棱锥的体积为\frac{4\sqrt{2}}{3}，则该半球的体积为．（ ）| A． | \frac{4\sqrt{2}}{3}π | B． | \frac{8\sqrt{2}}{3}π | C． | \frac{32\sqrt{2}}{3}π | D． | \frac{64\sqrt{2}}{3}π |