题目内容
已知幂函数y=x3m-9(m∈N*)的图象关于y轴对称,且在(0,+∞)上是减函数.
(1)求m的值;
(2)求满足不等式(a+1)- <(3-2a)-
<(3-2a)- 的实数a的取值范围.
的实数a的取值范围.
(1)求m的值;
(2)求满足不等式(a+1)-
 <(3-2a)-
<(3-2a)- 的实数a的取值范围.
的实数a的取值范围.(1)m=1(2)a<-1或 <a<
<a<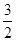
 <a<
<a<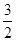
(1)因为函数y=x3m-9在(0,+∞)上是减函数,所以3m-9<0,所以m<3.
因为m∈N*,所以m=1或2.
又函数图象关于y轴对称,所以3m-9是偶数,所以m=1.
(2)不等式(a+1)- <(3-2a)-
<(3-2a)- 即为(a+1)-
即为(a+1)- <(3-2a)-
<(3-2a)- .
.
结合函数y=x- 的图象和性质知:
的图象和性质知:
a+1>3-2a>0或0>a+1>3-2a或a+1<0<3-2a.
解得a<-1或 <a<
<a<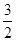 ,
,
即实数a的取值范围是a<-1或 <a<
<a<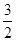 .
.
因为m∈N*,所以m=1或2.
又函数图象关于y轴对称,所以3m-9是偶数,所以m=1.
(2)不等式(a+1)-
 <(3-2a)-
<(3-2a)- 即为(a+1)-
即为(a+1)- <(3-2a)-
<(3-2a)- .
.结合函数y=x-
 的图象和性质知:
的图象和性质知:a+1>3-2a>0或0>a+1>3-2a或a+1<0<3-2a.
解得a<-1或
 <a<
<a<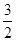 ,
,即实数a的取值范围是a<-1或
 <a<
<a<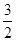 .
.
练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
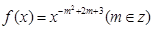 为偶函数,且在区间
为偶函数,且在区间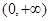 上是单调增函数
上是单调增函数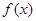 的解析式;
的解析式;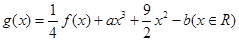 ,其中
,其中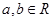 .若函数
.若函数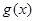 仅在
仅在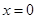 处有极值,求
处有极值,求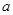 的取值范围.
的取值范围. 的图像经过点
的图像经过点 ,则
,则 的值等于
的值等于
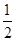
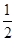 四个值,则对应于曲线C1,C2,C3,C4的n值依次为( )
四个值,则对应于曲线C1,C2,C3,C4的n值依次为( )
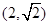 ,则 f(4)= .
,则 f(4)= . 的图像过点
的图像过点 ,若
,若 ,则实数
,则实数 的值为( )
的值为( )


