题目内容
已知集合A={(x,y)|sin(x+y)>0,且x2+y2≤π},则由集合A中的点所构成的平面图形的面积为
- A.
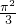
- B.π
- C.

- D.
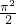
D
分析:由sin(x+y)>0可得2kπ<x+y<2kπ+π,由(0,0)到直线x+y=的距离d=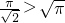 ,可得直线x+y=π与圆x2+y2=π相离,根据题意当k=0时与x2+y2=π有公共部分,与圆围成的图象如图所示的阴影部分,从而可求面积
,可得直线x+y=π与圆x2+y2=π相离,根据题意当k=0时与x2+y2=π有公共部分,与圆围成的图象如图所示的阴影部分,从而可求面积
解答:由sin(x+y)>0可得2kπ<x+y<2kπ+π
(0,0)到直线x+y=的距离d=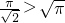 ,所以直线x+y=π与圆x2+y2=π相离
,所以直线x+y=π与圆x2+y2=π相离
根据题意当k=0时与x2+y2=π有公共部分,与圆围成的图象如图所示的阴影部分,是圆的一半,
则面积
故选D.
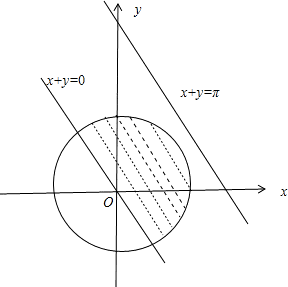
点评:本题主要考查了二元不等式表示平面区域,解题的关键是要由三角不等式求出x+y的范围,结合直线与圆的距离进行求解.
分析:由sin(x+y)>0可得2kπ<x+y<2kπ+π,由(0,0)到直线x+y=的距离d=
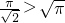 ,可得直线x+y=π与圆x2+y2=π相离,根据题意当k=0时与x2+y2=π有公共部分,与圆围成的图象如图所示的阴影部分,从而可求面积
,可得直线x+y=π与圆x2+y2=π相离,根据题意当k=0时与x2+y2=π有公共部分,与圆围成的图象如图所示的阴影部分,从而可求面积解答:由sin(x+y)>0可得2kπ<x+y<2kπ+π
(0,0)到直线x+y=的距离d=
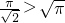 ,所以直线x+y=π与圆x2+y2=π相离
,所以直线x+y=π与圆x2+y2=π相离根据题意当k=0时与x2+y2=π有公共部分,与圆围成的图象如图所示的阴影部分,是圆的一半,
则面积

故选D.
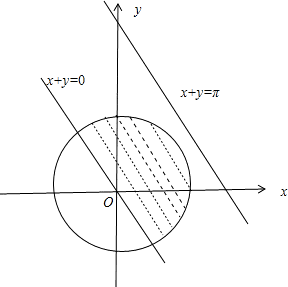
点评:本题主要考查了二元不等式表示平面区域,解题的关键是要由三角不等式求出x+y的范围,结合直线与圆的距离进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目