题目内容
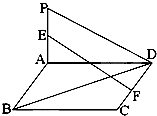 (2012•怀化二模)如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,∠PAD=
(2012•怀化二模)如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,∠PAD=| π | 2 |
(1)求证:PC⊥BD
(2)求直线EF与面PAD所成角的余弦值.
分析:(1)利用线面垂直,证明线线垂直,即证BD⊥面PAC,可得PC⊥BD;
(2)根据面PAD⊥面ABCD,且CD⊥AD,所以CD⊥面PAD,可得EF在面PAD上的射影是ED,所以∠FED为所求,在直角三角形FDE中,即可求直线EF与面PAD所成角的余弦值.
(2)根据面PAD⊥面ABCD,且CD⊥AD,所以CD⊥面PAD,可得EF在面PAD上的射影是ED,所以∠FED为所求,在直角三角形FDE中,即可求直线EF与面PAD所成角的余弦值.
解答:(1)证明:因为面PAD⊥面ABCD,且PA⊥AD,所以PA⊥面ABCD,因为BD?面ABCD,所以PA⊥BD-----------------(3分)
因为底面ABCD是正方形,所以BD⊥AC
又因PA和AC是面PAC上两相交直线,所以BD⊥面PAC,所以PC⊥BD-------(6分)
(2)解:因为面PAD⊥面ABCD,且CD⊥AD,所以CD⊥面PAD,
故EF在面PAD上的射影是ED,所以∠FED为所求----------(8分)
设PA=AD=b,在直角三角形FDE中,DF=
CD=
b,DE=
=
=
b
所以EF=
=
=
b-------------(10分)
所以 cos∠FED=
=
=
所以直线EF与面PAD所成角的余弦值为
---------------------(12分)
因为底面ABCD是正方形,所以BD⊥AC
又因PA和AC是面PAC上两相交直线,所以BD⊥面PAC,所以PC⊥BD-------(6分)
(2)解:因为面PAD⊥面ABCD,且CD⊥AD,所以CD⊥面PAD,
故EF在面PAD上的射影是ED,所以∠FED为所求----------(8分)
设PA=AD=b,在直角三角形FDE中,DF=
| 1 |
| 2 |
| 1 |
| 2 |
| EA2+AD2 |
|
| ||
| 2 |
所以EF=
| DE2+DF2 |
|
| ||
| 2 |
所以 cos∠FED=
| DE |
| EF |
| ||||
|
| ||
| 6 |
所以直线EF与面PAD所成角的余弦值为
| ||
| 6 |
点评:本题考查线面垂直、线线垂直,考查线面角,解题的关键是正确作出线面角,掌握线线垂直的判定方法.

练习册系列答案
相关题目
 (2012•怀化二模)对于大于或等于2的自然数m的n次幂进行如图方式的“分裂”.仿此,52的“分裂”中最大的数是
(2012•怀化二模)对于大于或等于2的自然数m的n次幂进行如图方式的“分裂”.仿此,52的“分裂”中最大的数是
 (2012•怀化二模)某算法的程序框图如图所示,若输出的结果为1,则输入的实数x的值是
(2012•怀化二模)某算法的程序框图如图所示,若输出的结果为1,则输入的实数x的值是 (2012•怀化二模)如图,一个树形图依据下列规律不断生长:1个空心圆点到下一行仅生长出1个实心圆点,1个实心圆点到下一行生长出1个实心圆点和1个空心圆点.则第8行的实心圆点的个数是
(2012•怀化二模)如图,一个树形图依据下列规律不断生长:1个空心圆点到下一行仅生长出1个实心圆点,1个实心圆点到下一行生长出1个实心圆点和1个空心圆点.则第8行的实心圆点的个数是