Question

【题目】如图,已知抛物线和,过抛物线上一点作两条直线与分别相切于两点,分别交抛物线于两点.

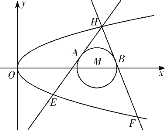
(1)当的角平分线垂直轴时,求直线的斜率；

(2)若直线在轴上的截距为,求的最小值.

Answer 1

【答案】（1）；（2）-11.

【解析】

（1）法一：根据当∠AHB的角平分线垂直x轴时，点H（4，2），可得kHE=﹣kHF，设E（x1，y1），F（x2，y2），可得y1+y2=﹣2yH=﹣4，从而可求直线EF的斜率；

法二：求得直线HA的方程为y=x﹣4+2，与抛物线方程联立，求出E，F的坐标，从而可求直线EF的斜率；

（2）法一：设A（x1，y1），B（x2，y2），求出直线HA的方程，直线HB的方程，从而可得直线AB的方程，令x=0，可得t=4y0﹣（y0≥1），再利用导数法，即可求得t的最小值．

法二：求以H为圆心，HA为半径的圆方程，⊙M方程，两方程相减，可得直线AB的方程，当x=0时，直线AB在y轴上的截距t=4m﹣（m≥1），再利用导数法，即可求得t的最小值．

(1)法一：∵当的角平分线垂直轴时,点,

∴,

设,

∴,∴

∴,

.

法二：∵当的角平分线垂直轴时,点,

∴,可得 ,

∴直线的方程为,

联立方程组得,

∵,∴ .

同理可得 .

∴.

(2)法一：

设点,,.

以为圆心,为半径的圆方程为：,①

方程：.②

①-②得：直线的方程为.

当时,直线在轴上的截距,

∵关于的函数在[1,+∞)单调递增,

∴.

法二：设,∵,∴,

可得,直线的方程为,

同理,直线的方程为,

∴ ,

∴直线的方程为,

令,可得,

∵关于的函数在[1,+∞)单调递增,

∴.