题目内容
.已知函数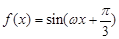 (
(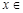 R,
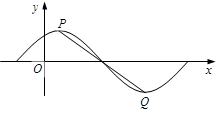
R,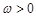 )的图象如图,P是图象的最高点,Q是图象的最低点.且
)的图象如图,P是图象的最高点,Q是图象的最低点.且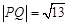 .
.
(Ⅰ)求函数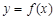 的解析式;
的解析式;
(Ⅱ)将函数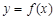 图象向右平移1个单位后得到函数
图象向右平移1个单位后得到函数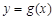 的图象,当
的图象,当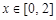 时,求函数
时,求函数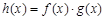 的最大值.
的最大值.
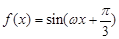 (
(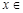 R,
R,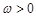 )的图象如图,P是图象的最高点,Q是图象的最低点.且
)的图象如图,P是图象的最高点,Q是图象的最低点.且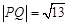 .
.
(Ⅰ)求函数
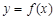 的解析式;
的解析式;(Ⅱ)将函数
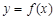 图象向右平移1个单位后得到函数
图象向右平移1个单位后得到函数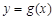 的图象,当
的图象,当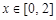 时,求函数
时,求函数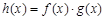 的最大值.
的最大值.(Ⅰ)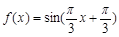 ;(Ⅱ)即
;(Ⅱ)即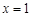 时
时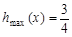 .
.
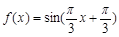 ;(Ⅱ)即
;(Ⅱ)即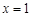 时
时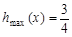 .
.本试题主要是考查了三角函数图像与性质的综合运用,以及三角函数图像变换的综合运用。
(1)根据已知的条件可知,勾股定理可以得到点半个周期的长,得到w的值,然后得到振幅和初相的值。
(2)将函数化为单一三角函数,然后利用二倍角公式和自变量的取值范围可以得到三角函数的值域。
解:(Ⅰ)过点P作x 轴的垂线PM,过点Q作y 轴的垂线QM,
两直线交于点M.
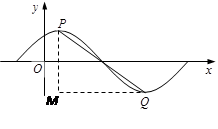
则由已知得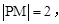
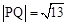 由勾股定理得
由勾股定理得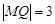
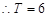 …………3分
…………3分
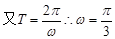
∴ 的解析式为
的解析式为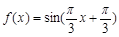 …………5分
…………5分
(Ⅱ)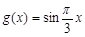 , …………7分
, …………7分
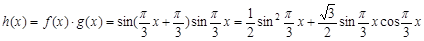
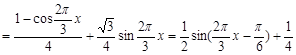 .…………11分
.…………11分
当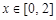 时,
时,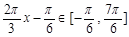 , ∴ 当
, ∴ 当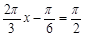 ,即
,即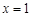 时
时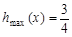 .14分
.14分
(1)根据已知的条件可知,勾股定理可以得到点半个周期的长,得到w的值,然后得到振幅和初相的值。
(2)将函数化为单一三角函数,然后利用二倍角公式和自变量的取值范围可以得到三角函数的值域。
解:(Ⅰ)过点P作x 轴的垂线PM,过点Q作y 轴的垂线QM,
两直线交于点M.

则由已知得
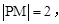
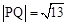 由勾股定理得
由勾股定理得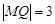
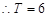 …………3分
…………3分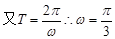
∴
 的解析式为
的解析式为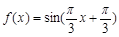 …………5分
…………5分(Ⅱ)
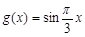 , …………7分
, …………7分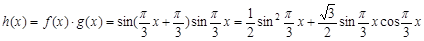
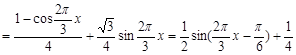 .…………11分
.…………11分当
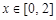 时,
时,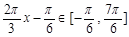 , ∴ 当
, ∴ 当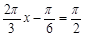 ,即
,即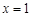 时
时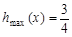 .14分
.14分
练习册系列答案
相关题目
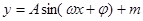 的最大值为
的最大值为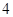 ,最小值为
,最小值为 ,最小正周期为
,最小正周期为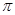 ,直线
,直线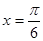 是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
是其图象的一条对称轴,则下面各式中符合条件的解析式是( )



 (
( )
) 的最小正周期;
的最小正周期; cos2x+sinxcosx-
cos2x+sinxcosx- 的周期是( )
的周期是( )

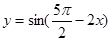 是偶函数;②函数
是偶函数;②函数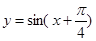 在闭区间
在闭区间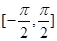 上是增函数;
上是增函数;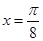 是函数
是函数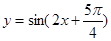 图象的一条对称轴;
图象的一条对称轴;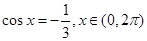 ,则
,则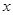 =arccos(-
=arccos(-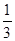 )或π+arccos(-
)或π+arccos(- 4sin x
4sin x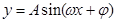 在一个周期内的图象,此函数的解析式为可为( )
在一个周期内的图象,此函数的解析式为可为( )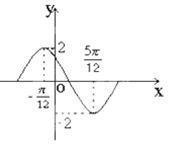
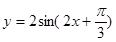
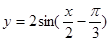
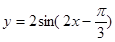
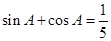
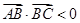
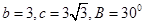
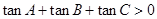
 的值为 .
的值为 .