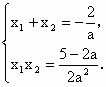题目内容
在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点,已知|AB|=2|OA|,且点B的纵坐标大于零.
(1)求向量![]() 的坐标;
的坐标;
(2)求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程;
(3)是否存在实效a,使抛物线y=ax2-1上总有关于直线OB对称的两个点?若不存在,说明理由;若存在,求a的取值范围.
答案:
解析:
解析:
|
解:(1)设 即 解得 因为 故 (2)由 由条件可知圆的标准方程为 (x-3)2+(y+1)2=10. ∴圆心为(3,-1),半径为 设圆心(3,-1)关于直线OB的对称点为(x,y),则 故所求圆的方程为(x-1)2+(y-3)2=10. (3)设P(x1,y1),Q(x2,y2)为抛物线上关于直线OB对称的两点,则 即x1,x2为方程x2+ 于是由Δ= 故当a> |

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
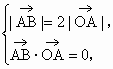
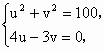
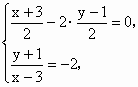 解得
解得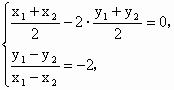 得
得