题目内容
已知x、y满足约束条件 ,Z=2x+y的最大值是 ( )
,Z=2x+y的最大值是 ( )
| A.-5 | B.3 | C. | D.5 |
B
解析试题分析:
先画出线性约束条件对应的可行域,再为目标函数值Z赋予几何意义:纵截距,数形结合找到最优解,代入目标函数即可得目标函数最值。
解:画出可行域如图三角形ABC区域: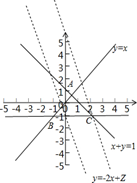 ,
,
目标函数 Z=2x+y可看做直线l:y=-2x+Z的纵截距,如图可知当直线l过点C时,Z最大,由x+y=1,y=-1得C(2,-1),∴Zmax=2×2-1=3,故选B
考点:线性规划问题
点评:本题考查了线性规划问题的解法,数形结合的思想方法,准确画出可行域,确定目标函数的平移方向是解决本题的关键

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
已知甲、乙两种不同品牌的PVC管材都可截成A、B、C三种规格的成品配件,且每种PVC管同时截得三种规格的成品个数如下表:
| | A规格成品(个) | B规格成品(个) | C规格成品(个) |
| 品牌甲(根) | 2 | 1 | 1 |
| 品牌乙(根) | 1 | 1 | 2 |
A.70元 B.75元 C.80元 D.95元
若变量 满足约束条件
满足约束条件 且
且 的最大值为
的最大值为 ,最小值为
,最小值为 ,则
,则 的值是
的值是
A. | B. | C. | D. |
设集合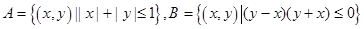 ,
,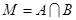 ,
,
若动点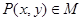 ,则
,则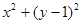 的取值范围是( )
的取值范围是( )
A.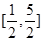 | B.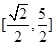 | C.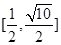 | D.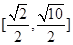 |
设变量 满足约束条件
满足约束条件 ,则
,则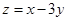 的最小值为
的最小值为
| A.-2 | B.-4 | C.-6 | D.-8 |
已知变量x、y满足约束条件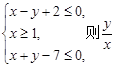 的取值范围是( )
的取值范围是( )
A.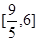 | B.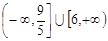 | C.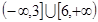 | D.[3,6] |
某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元。该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是 ( )
| A.12万元 | B.20万元 | C.25万元 | D.27万元 |
已知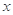 、
、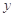 满足约束条件
满足约束条件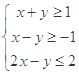 , 若目标函数
, 若目标函数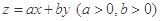 的最大值为7, 则
的最大值为7, 则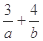 的最小值为( )
的最小值为( )
| A.14 | B.7 | C.18 | D.13 |
已知变量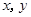 满足约束条件
满足约束条件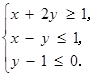 则
则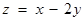 的最大值为
的最大值为
A.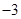 | B. | C. | D.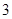 |