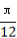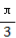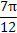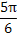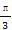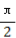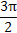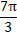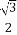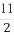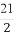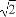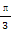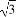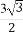题目内容
已知函数f(x)=sin(2x+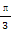
).
(1)求函数y=f(x)的单调递减区间.
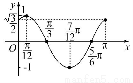
(2)画出函数y=f(x)在区间[0,π]上的图象.
(1) [kπ+
,kπ+
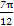](k∈Z) (2)见解析
【解析】(1)由2kπ+
≤2x+
≤2kπ+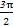
(k∈Z),
得kπ+≤x≤kπ+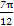(k∈Z).
∴函数的单调递减区间是[kπ+,kπ+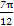](k∈Z).
(2)∵0≤x≤π,∴≤2x+≤
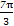.列表如下:
x | 0 |
|
|
|
| π |
2x+ |
|
| π |
| 2π |
|
y |
| 1 | 0 | -1 | 0 |
|
画出图象如图所示:
练习册系列答案
名校课堂系列答案
相关题目
