题目内容
对于定义域为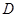 的函数
的函数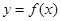 ,若同时满足:
,若同时满足:
① 在
在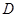 内单调递增或单调递减;
内单调递增或单调递减;
②存在区间[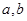 ]
]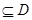 ,使
,使 在
在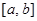 上的值域为
上的值域为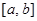 ;
;
那么把函数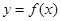 (
(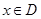 )叫做闭函数.
)叫做闭函数.
(1) 求闭函数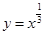 符合条件②的区间
符合条件②的区间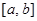 ;
;
(2) 若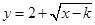 是闭函数,求实数
是闭函数,求实数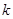 的取值范围.
的取值范围.
(1)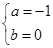 或
或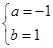 或
或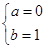 ,(2)
,(2)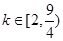 .
.
解析试题分析:(1)新定义的问题,首先按新定义进行等价转化. 由题意,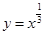 在[
在[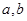 ]上递增,则
]上递增,则
 解得
解得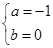 或
或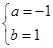 或
或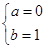 ,(2)若
,(2)若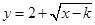 是闭函数,则存在区间[
是闭函数,则存在区间[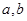 ],在区间[
],在区间[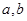 ]上,函数
]上,函数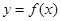 的值域为[
的值域为[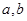 ],可证明函数
],可证明函数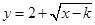 在定义域内单调递增,因此
在定义域内单调递增,因此 ∴
∴ 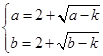 ∴
∴ 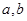 为方程
为方程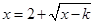 的两个实数根. 即方程
的两个实数根. 即方程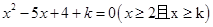 有两个不相等的实根.
有两个不相等的实根. 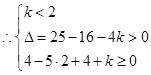 或
或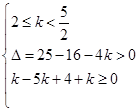 解得
解得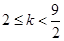 ,综上所述,
,综上所述,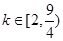
试题解析:[解析](1)由题意,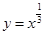 在[
在[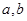 ]上递增,则
]上递增,则 ,
,
解得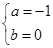 或
或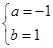 或
或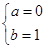
所以,所求的区间为[-1,0]或[-1,1]或[0,1] . 6分(解得一个区间得2分)
(2)若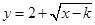 是闭函数,则存在区间[
是闭函数,则存在区间[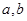 ],在区间[
],在区间[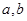 ]上,
]上,
函数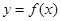 的值域为[
的值域为[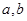 ] 6分
] 6分
容易证明函数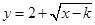 在定义域内单调递增,
在定义域内单调递增,
∴ 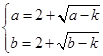 8分
8分
∴ 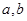 为方程
为方程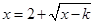 的两个实数根. 10分
的两个实数根. 10分
即方程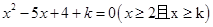 有两个不相等的实根.
有两个不相等的实根. 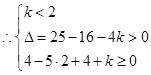 或
或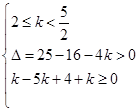 14分
14分
解得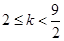 ,综上所述,
,综上所述,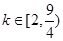 16分
16分
考点:新定义,函数与方程

练习册系列答案
相关题目
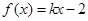 满足
满足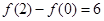 。
。 的解析式;
的解析式;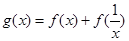 的值域。
的值域。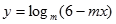 在
在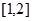 上单调递减.
上单调递减. 在
在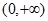 内有一个零点.若p或q为真,p且q为假,求实数m的取值范围.
内有一个零点.若p或q为真,p且q为假,求实数m的取值范围.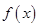 是定义在
是定义在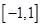 上的奇函数,在
上的奇函数,在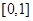 上
上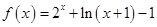 .
.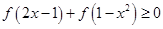 .
.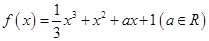 .
.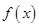 的单调区间;
的单调区间;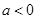 时,试讨论是否存在
时,试讨论是否存在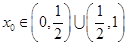 ,使得
,使得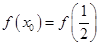 .
.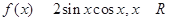 .
. 的最小正周期;
的最小正周期;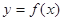 的奇偶性, 并说明理由。
的奇偶性, 并说明理由。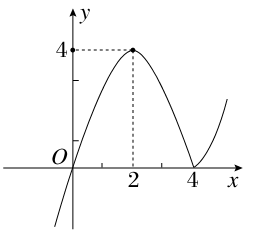
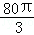 立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
立方米,且l≥2r.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为c(c>3)千元.设该容器的建造费用为y千元.
 ,若
,若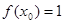 ,则
,则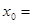 .
.