题目内容
有定点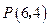 及定直线
及定直线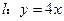 ,
, 是
是 上在第一象限内的点,
上在第一象限内的点,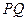 交
交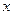 轴的正半轴于
轴的正半轴于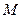 点,问点
点,问点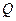 在什么位置时,
在什么位置时,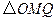 的面积最小,并求出最小值.
的面积最小,并求出最小值.
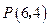 及定直线
及定直线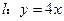 ,
,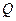 是
是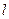 上在第一象限内的点,
上在第一象限内的点,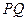 交
交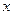 轴的正半轴于
轴的正半轴于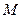 点,问点
点,问点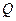 在什么位置时,
在什么位置时,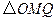 的面积最小,并求出最小值.
的面积最小,并求出最小值. |
当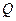 点坐标为
点坐标为 时,
时,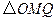 面积最小,且最小值为40
面积最小,且最小值为40
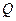 点坐标为
点坐标为 时,
时,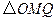 面积最小,且最小值为40
面积最小,且最小值为40当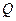 点的坐标为
点的坐标为 时,
时,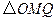 面积最小为40.
面积最小为40.
解析:设点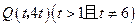 ,
,
 直线
直线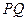 的方程为
的方程为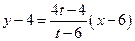 ,令
,令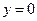 ,得
,得 .
.
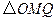 的面积
的面积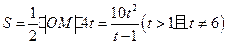 ,即
,即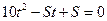 .
.

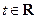 ,
, 关于
关于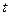 的一元二次方程有实根,
的一元二次方程有实根,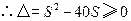 ,
,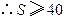 .
.
当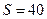 时,
时,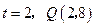 ,而当
,而当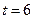 时,
时,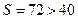 ,不合要求.
,不合要求.
故当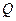 点坐标为
点坐标为 时,
时,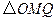 面积最小,且最小值为40.
面积最小,且最小值为40.
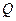 点的坐标为
点的坐标为 时,
时,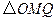 面积最小为40.
面积最小为40.解析:设点
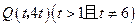 ,
, 直线
直线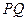 的方程为
的方程为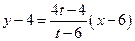 ,令
,令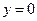 ,得
,得 .
.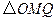 的面积
的面积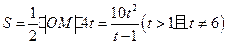 ,即
,即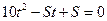 .
.
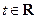 ,
, 关于
关于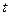 的一元二次方程有实根,
的一元二次方程有实根,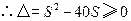 ,
,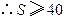 .
.当
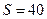 时,
时,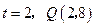 ,而当
,而当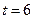 时,
时,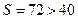 ,不合要求.
,不合要求.故当
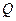 点坐标为
点坐标为 时,
时,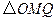 面积最小,且最小值为40.
面积最小,且最小值为40.
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
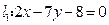 ,
,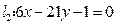 ,
,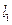 与
与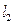 是否平行?若平行,求
是否平行?若平行,求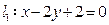 ,
, 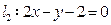 .
.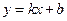 中,当
中,当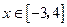 时,
时,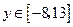 ,求此直线的方程.
,求此直线的方程.

 B
B 
 D
D 