题目内容
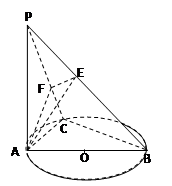
已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的个数是 ( )
①PA⊥AD
②平面ABC⊥平面PBC
③直线BC∥平面PAE
④直线PD与平面ABC所成角为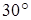
 .1个
.1个 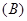 .2个
.2个 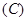 .3个
.3个 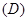 .4个
.4个
①PA⊥AD
②平面ABC⊥平面PBC
③直线BC∥平面PAE
④直线PD与平面ABC所成角为
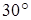
 .1个
.1个  .2个
.2个  .3个
.3个  .4个
.4个A
知识点分析:本题考查立体集合中的各种关系:线线关系、线面关系、面面关系以及线面角,考生应该掌握各种关系的判定、性质及相关计算。
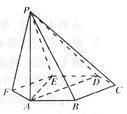
思路分析:本题应该先画图,采取‘一做二证三计算’的策略
解:依题画图如图.对①,由于PA⊥平面ABC且AD 在平面ABC内,所以①对;对于②,观察图可知平面PBC不垂直平面ABC,具体证明可以延长BC过A做AG垂直BC于G则由射影定理可知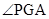 为A-BC-P的二面角改角的正切值为
为A-BC-P的二面角改角的正切值为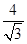 不是直角;对于③,可以用反证法,若BC∥平面PAE,则BC∥AE,而由正六边形的性质可知BC与AE不可能平行所以③错;对于④、显然PD是斜线
不是直角;对于③,可以用反证法,若BC∥平面PAE,则BC∥AE,而由正六边形的性质可知BC与AE不可能平行所以③错;对于④、显然PD是斜线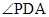 即为所求的线面角,由正六边形可知AD为其外接圆的直径
即为所求的线面角,由正六边形可知AD为其外接圆的直径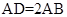 所以
所以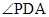 正切值为1,该线面角应为
正切值为1,该线面角应为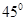 。所以答案选择A
。所以答案选择A
点评:本题以立体图形为载体,综合考查了立体几何的知识,综合性较强。

思路分析:本题应该先画图,采取‘一做二证三计算’的策略
解:依题画图如图.对①,由于PA⊥平面ABC且AD 在平面ABC内,所以①对;对于②,观察图可知平面PBC不垂直平面ABC,具体证明可以延长BC过A做AG垂直BC于G则由射影定理可知
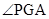 为A-BC-P的二面角改角的正切值为
为A-BC-P的二面角改角的正切值为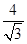 不是直角;对于③,可以用反证法,若BC∥平面PAE,则BC∥AE,而由正六边形的性质可知BC与AE不可能平行所以③错;对于④、显然PD是斜线
不是直角;对于③,可以用反证法,若BC∥平面PAE,则BC∥AE,而由正六边形的性质可知BC与AE不可能平行所以③错;对于④、显然PD是斜线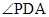 即为所求的线面角,由正六边形可知AD为其外接圆的直径
即为所求的线面角,由正六边形可知AD为其外接圆的直径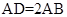 所以
所以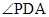 正切值为1,该线面角应为
正切值为1,该线面角应为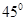 。所以答案选择A
。所以答案选择A点评:本题以立体图形为载体,综合考查了立体几何的知识,综合性较强。

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
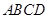 中,对角线
中,对角线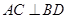 ,且
,且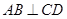 ,则点
,则点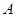 在
在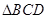 内的射影
内的射影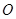 是
是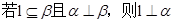
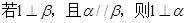
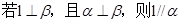
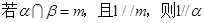
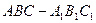 中,底面
中,底面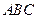 是边长为2的正三角形,侧棱长为3,且侧棱
是边长为2的正三角形,侧棱长为3,且侧棱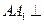 面
面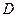 是
是 的中点.
的中点.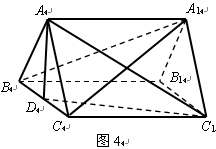
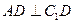 ;
;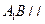 平面
平面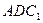 .
. α,l
α,l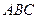 为底面的棱柱被平面
为底面的棱柱被平面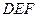 所截而得,已
所截而得,已 知
知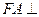 平面
平面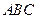 ,
,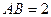 ,
,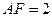 ,
,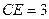 ,
,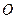 为
为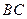 的中点,
的中点,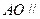 面
面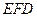 .
.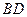 的长;
的长;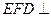 面
面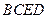 ;
;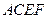 相交所成锐角二面角的余弦值.
相交所成锐角二面角的余弦值.
 是三条不重合直线,
是三条不重合直线, 、
、 、
、 是三个不重合平面,下列说法:
是三个不重合平面,下列说法: ,
,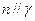

 ; ②
; ②  ,
,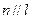
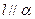 ,
,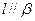
 ;
; ,
,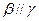

 ;⑥
;⑥ 
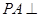 圆
圆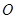 所在平面,
所在平面,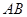 是圆
是圆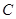 是圆
是圆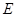 、
、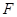 分别是点
分别是点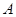 在
在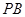 、
、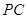 上的射影,给出下列结论:①
上的射影,给出下列结论:①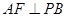 ;②
;②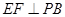 ;③
;③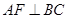 ;④
;④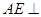 平面
平面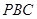 ,其中正确的结论是____________。
,其中正确的结论是____________。