题目内容
5．在直角三角形ABC中，∠C=$\frac{π}{2}$，AB=2，AC=1，若$\overrightarrow{AD}=\frac{3}{2}\overrightarrow{AB}$，则$\overrightarrow{CD}•\overrightarrow{CB}$=（ ）| A． | $\frac{9}{2}$ | B． | 5 | C． | 6 | D． | 9 |
分析 直角三角形中的边角关系求得BC、BD，∠CBD的值，利用余弦定理求得CD、cos∠BCD 的值，再根据两个向量的数量积的定义求得$\overrightarrow{CD}•\overrightarrow{CB}$=CD•CB•cos∠BCD 的值．
解答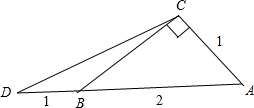 
解：在直角三角形ABC中，∠C=$\frac{π}{2}$，AB=2，AC=1，若$\overrightarrow{AD}=\frac{3}{2}\overrightarrow{AB}$，
则AD=3，∠ABC=$\frac{π}{6}$，∠CBD=$\frac{5π}{6}$，∴BD=1，CB=$\sqrt{{AB}^{2}{-AC}^{2}}$=$\sqrt{3}$．
△BCD中，由余弦定理可得CD2=BD2+BC2-2BD•BC•cos$\frac{5π}{6}$=3+1-2×1×$\sqrt{3}$×（-$\frac{\sqrt{3}}{2}$）=7，∴CD=$\sqrt{7}$．
由cos∠BCD=$\frac{{CD}^{2}{+BC}^{2}{-BD}^{2}}{2CD•BC}$=$\frac{3\sqrt{21}}{14}$．
则$\overrightarrow{CD}•\overrightarrow{CB}$=CD•CB•cos∠BCD=$\sqrt{7}$×$\sqrt{3}$×$\frac{3\sqrt{21}}{14}$=$\frac{9}{2}$，
故选：A．
点评 本题主要考查直角三角形中的边角关系，余弦定理的应用，两个向量的数量积的定义，属于中档题．
练习册系列答案
相关题目
16．已知等比数列{an}的前10项的积为32，则以下说法中正确的个数是（ ）
①数列{an}的各项均为正数； ②数列{an}中必有小于$\sqrt{2}$的项；
③数列{an}的公比必是正数； ④数列{an}中的首项和公比中必有一个大于1．
①数列{an}的各项均为正数； ②数列{an}中必有小于$\sqrt{2}$的项；
③数列{an}的公比必是正数； ④数列{an}中的首项和公比中必有一个大于1．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
10．某同学用“五点法”画函数f（x）=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）在某一个周期内的图象时，列表并填入的部分数据如下表：
（Ⅰ）请求出上表中的xl，x2，x3，并直接写出函数f（x）的解析式．
（Ⅱ）将f（x）的图象沿x釉向右平移$\frac{2}{3}$个单位得到函数g（x），若函数g（x）在x∈[0，m]（其中m∈（2，4））上的值域为[-$\sqrt{3}$，$\sqrt{3}$]，且此时其图象的最高点和最低点分别为P，Q，求$\overrightarrow{OQ}$与$\overrightarrow{QP}$夹角θ的大小．
| x | x1 | $\frac{1}{3}$ | x2 | $\frac{7}{3}$ | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin（ωx+φ）+B | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
（Ⅱ）将f（x）的图象沿x釉向右平移$\frac{2}{3}$个单位得到函数g（x），若函数g（x）在x∈[0，m]（其中m∈（2，4））上的值域为[-$\sqrt{3}$，$\sqrt{3}$]，且此时其图象的最高点和最低点分别为P，Q，求$\overrightarrow{OQ}$与$\overrightarrow{QP}$夹角θ的大小．
14．已知直线l与抛物线y2=8x交于A、B两点，且l经过抛物线的焦点F，A点的坐标为（8，8），则线段AB的中点到准线的距离是（ ）
| A． | $\frac{17}{4}$ | B． | $\frac{7}{2}$ | C． | $\frac{25}{4}$ | D． | $\frac{27}{4}$ |