题目内容
给出下列四个命题,其中所有正确命题的序号为
①当a为任意实数时,直线(a-1)x-y+2a+1=0恒过定点P(-2,3);
②已知双曲线的右焦点为(5,0),一条渐近线方程为2x-y=0,则双曲线的标准方程是
-
=1;
③抛物线y=ax2(a≠0)的焦点坐标为(
,0);
④曲线C:
+
=1不可能表示椭圆.
①②
①②
.①当a为任意实数时,直线(a-1)x-y+2a+1=0恒过定点P(-2,3);
②已知双曲线的右焦点为(5,0),一条渐近线方程为2x-y=0,则双曲线的标准方程是
| x2 |
| 5 |
| y2 |
| 20 |
③抛物线y=ax2(a≠0)的焦点坐标为(
| 1 |
| 4a |
④曲线C:
| x2 |
| 4-k |
| y2 |
| k-1 |
分析:①中直线可化为(x+2)a+(-x-y+1)=0,要使a为任意实数时,此式恒成立,则有
得
,故①正确;②中根据渐近线方程求得a和b的关系,进而根据焦距求得a和b,双曲线方程可得,判断②正确;③把抛物线方程整理成标准方程,进而根据抛物线的性质可得抛物线的焦点在y轴上,判断③错误;④当4-k>0,k-1>0且4-k≠k-1时,曲线表示椭圆,故④错误.
|
|
解答:解:对于①,直线(a-1)x-y+2a+1=0可化为(x+2)a+(-x-y+1)=0,
要使a为任意实数时,此式恒成立,则有
得
,
∴直线(a-1)x-y+2a+1=0恒过定点P(-2,3),
故①正确;
②对于依题意知
=2,a2+b2=25求得a=
,b=2
,故可知结论②正确;
③整理抛物线方程得x2=
y,根据抛物线性质可知,抛物线的焦点在y轴上,故③错误;
④当4-k>0,k-1>0且4-k≠k-1时,曲线表示椭圆,故④错误.
故答案为:①②
要使a为任意实数时,此式恒成立,则有
|
|
∴直线(a-1)x-y+2a+1=0恒过定点P(-2,3),
故①正确;
②对于依题意知
| b |
| a |
| 5 |
| 5 |
③整理抛物线方程得x2=
| 1 |
| a |
④当4-k>0,k-1>0且4-k≠k-1时,曲线表示椭圆,故④错误.
故答案为:①②
点评:本题以圆锥曲线的性质为载体,综合考查了圆锥曲线的基本性质.熟练掌握圆锥曲线的性质是正确解题的基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


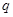 是等比数列
是等比数列 的公比,则“数列
的公比,则“数列 ”的既不充分也不必要条件;
”的既不充分也不必要条件; 上的函数
上的函数 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意 必有
必有 ;
; 满足
满足 ,则
,则 的一个正周期为
的一个正周期为 ;
; 与
与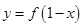 图像关于
图像关于 对称.
对称.