题目内容
给出下列四个命题
①命题“?x∈R,cosx>0”的否定是“?x0∈R,cosx0≤0”
②若0<a<1,则方程x2+ax-3=0只有一个实数根;
③对于任意实数x,有f(-x)=f(x),且当x>0时,f′(x)>0,则当x<0时,f′(x)<0;
④一个矩形的面积为S,周长为l,则有序实数对(6,8)可作为(S,l)取得的一组实数对,其正确命题的序号是
①命题“?x∈R,cosx>0”的否定是“?x0∈R,cosx0≤0”
②若0<a<1,则方程x2+ax-3=0只有一个实数根;
③对于任意实数x,有f(-x)=f(x),且当x>0时,f′(x)>0,则当x<0时,f′(x)<0;
④一个矩形的面积为S,周长为l,则有序实数对(6,8)可作为(S,l)取得的一组实数对,其正确命题的序号是
①③
①③
.(填所有正确的序号)分析:①利用全称命题的否定是特称命题即可判断其正误;
②在同一坐标系中利用y=ax(0<a<1)与y=3-x2的交点个数即可判断;
③利用偶函数在关于原点对称区间上的单调性即可判断其正误;
④依题意,可设该矩形的两边长为a,b,列式计算即可判断其正误;
②在同一坐标系中利用y=ax(0<a<1)与y=3-x2的交点个数即可判断;
③利用偶函数在关于原点对称区间上的单调性即可判断其正误;
④依题意,可设该矩形的两边长为a,b,列式计算即可判断其正误;
解答:解:①命题“?x∈R,cosx>0”的否定是“?x0∈R,cosx0≤0”正确;
②当0<a<l,y=ax为减函数,与y=3-x2交点个数是两个,即0<a<1时,方程x2+ax-3=0有两个实数根,故②错误;
③,由题意得,f(x)为偶函数,且在(0,+∞)上单调递增,故在(-∞,0)上单调递减,于是“当x<0时,f′(x)<0”正确;
④,设该矩形的两边长为a,b,则ab=6且2a+2b=8,
∴a2-4a+6=0,
∵△=16-24<0,
∴方程a2-4a+6=0无解,故④错误;
故答案为:①③.
②当0<a<l,y=ax为减函数,与y=3-x2交点个数是两个,即0<a<1时,方程x2+ax-3=0有两个实数根,故②错误;
③,由题意得,f(x)为偶函数,且在(0,+∞)上单调递增,故在(-∞,0)上单调递减,于是“当x<0时,f′(x)<0”正确;
④,设该矩形的两边长为a,b,则ab=6且2a+2b=8,
∴a2-4a+6=0,
∵△=16-24<0,
∴方程a2-4a+6=0无解,故④错误;
故答案为:①③.
点评:本题考查命题的真假判断与应用,考查命题间的关系,考查函数的零点与函数的性质,考查方程思想与转化思想的应用,属于中档题.

练习册系列答案
相关题目
 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: ,
, ,则
,则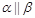 ;
; ,
, ,
, ,
, ,则
,则 ;
;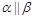 ,
, ,则
,则 ;
; ,
, ,
, ,
, ,则
,则 其中真命
其中真命