题目内容
12.已知函数f (x)=$\left\{\begin{array}{l}{e}^x-k,x≤0\\(1-k)x+k,x>0\end{array}$ 是R上的增函数,则实数k的取值范围是( )| A. | ( $\frac{1}{3}$,$\frac{2}{3}$ ) | B. | [$\frac{1}{3}$,$\frac{2}{3}$ ) | C. | ( $\frac{1}{2}$,$\frac{2}{3}$ ) | D. | [$\frac{1}{2}$,1 ) |
分析 根据分段函数的单调性的性质建立不等式关系即可.
解答 解:∵函数f(x)为增函数,
∴满足$\left\{\begin{array}{l}{1-k>0}\\{{e}^{0}-k≤k}\end{array}\right.$,即$\left\{\begin{array}{l}{k<1}\\{k≥\frac{1}{2}}\end{array}\right.$,
解得$\frac{1}{2}$≤k<1,
故选:D.
点评 本题主要考查函数单调性的应用,利用分段函数单调性的性质是解决本题的关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
3.下列程序的功能是( )


| A. | 求1×2×3×4×…×10000的值 | |
| B. | 求2×4×6×8×…×10000的值 | |
| C. | 求3×5×7×9×…×10001的值 | |
| D. | 求满足1×3×5×…×n>10000的最小正整数n |
17.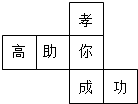 水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )
水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )
 水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )
水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )| A. | 左面,后面,上面 | B. | 后面,上面,左面 | C. | 上面,左面,后面 | D. | 后面,左面,上面 |