题目内容
(2011•浙江)设x,y为实数,若4x2+y2+xy=1,则2x+y的最大值是 _________ .
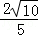
∵4x2+y2+xy=1
∴(2x+y)2﹣3xy=1
令t=2x+y则y=t﹣2x
∴t2﹣3(t﹣2x)x=1
即6x2﹣3tx+t2﹣1=0
∴△=9t2﹣24(t2﹣1)=﹣15t2+24≥0
解得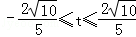
∴2x+y的最大值是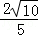
∴(2x+y)2﹣3xy=1
令t=2x+y则y=t﹣2x
∴t2﹣3(t﹣2x)x=1
即6x2﹣3tx+t2﹣1=0
∴△=9t2﹣24(t2﹣1)=﹣15t2+24≥0
解得
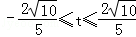
∴2x+y的最大值是
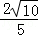

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
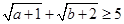 ,证明:
,证明: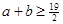
 的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 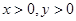 ,若
,若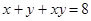 ,则
,则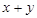 的最小值为 .
的最小值为 .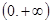 上的函数
上的函数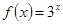 ,若
,若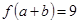 ,则
,则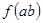 的最大值为______
的最大值为______ +
+ 的最小值是( )
的最小值是( )

 AB,tan∠FED=
AB,tan∠FED=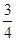 ,设AB=xm,BC=ym.
,设AB=xm,BC=ym.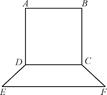
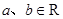 ,且
,且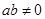 ,则下列结论恒成立的是 ( ).
,则下列结论恒成立的是 ( ).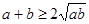
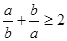
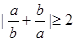
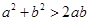
 有实根,则实数
有实根,则实数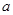 的取值范围是___________.[
的取值范围是___________.[