题目内容
函数 ,若数列
,若数列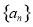 满足
满足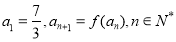 ,则
,则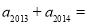
A. 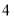 B.
B. 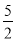 C.
C. 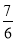 D.
D. 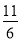
C
【解析】
试题分析:由题意可知
 ,从第三项开始是以3为周期的数列,∴
,从第三项开始是以3为周期的数列,∴
 .
.
考点:分段函数、周期性、数列递推公式.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
题目内容
函数 ,若数列
,若数列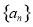 满足
满足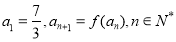 ,则
,则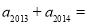
A. 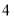 B.
B. 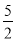 C.
C. 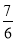 D.
D. 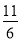
C
【解析】
试题分析:由题意可知
 ,从第三项开始是以3为周期的数列,∴
,从第三项开始是以3为周期的数列,∴
 .
.
考点:分段函数、周期性、数列递推公式.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案