题目内容
已知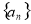 是等比数列,前
是等比数列,前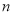 项和为
项和为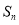 ,
,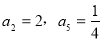 ,则
,则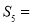
A.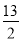 B.
B.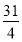
C.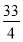 D.
D.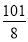
B
【解析】
试题分析:由已知条件可得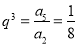 ,∴
,∴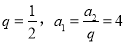 ,∴
,∴ .
.
考点:等比数列的定义、等比数列的前n项和.

练习册系列答案
相关题目
题目内容
已知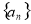 是等比数列,前
是等比数列,前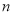 项和为
项和为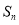 ,
,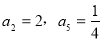 ,则
,则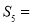
A.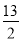 B.
B.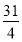
C.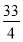 D.
D.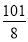
B
【解析】
试题分析:由已知条件可得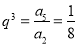 ,∴
,∴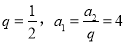 ,∴
,∴ .
.
考点:等比数列的定义、等比数列的前n项和.
