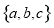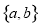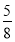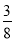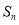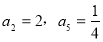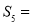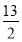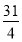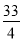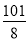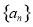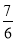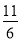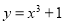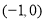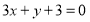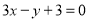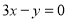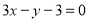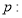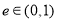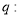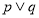题目内容
已知椭圆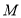 :
: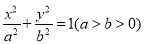 经过如下五个点中的三个点:
经过如下五个点中的三个点: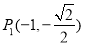 ,
,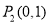 ,
,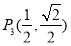 ,
,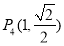 ,
,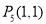 .
.
(Ⅰ)求椭圆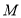 的方程;
的方程;
(Ⅱ)设点 为椭圆
为椭圆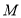 的左顶点,
的左顶点,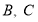 为椭圆
为椭圆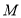 上不同于点
上不同于点 的两点,若原点在
的两点,若原点在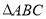 的外部,且
的外部,且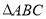 为直角三角形,求
为直角三角形,求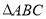 面积的最大值.
面积的最大值.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)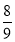
【解析】
试题分析:(Ⅰ)因为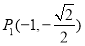 和
和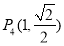 关于原点对称,由椭圆的对称性可知
关于原点对称,由椭圆的对称性可知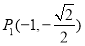 和
和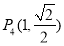 在椭圆上。因为
在椭圆上。因为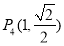 在椭圆上则
在椭圆上则 和
和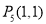 不在椭圆上。所以
不在椭圆上。所以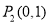 在椭圆上。解方程组可得
在椭圆上。解方程组可得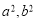 的值。(Ⅱ)需讨论哪个角为直角只讨论
的值。(Ⅱ)需讨论哪个角为直角只讨论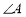 和
和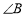 即可,因为点
即可,因为点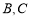 的位置没有固定,
的位置没有固定,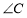 和
和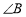 的情况相同。如当
的情况相同。如当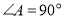 时,设直线
时,设直线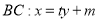 ,联立方程消去消去
,联立方程消去消去 得关于
得关于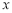 的一元二次方程,由韦达定理得根与系数的关系。根据
的一元二次方程,由韦达定理得根与系数的关系。根据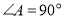 ,则直线垂直其斜率相乘等于
,则直线垂直其斜率相乘等于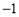 ,列式计算可得
,列式计算可得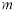 ,
,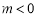 则说明原点在
则说明原点在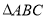 的外部,符合条件,否则不符合条件舍掉。在求
的外部,符合条件,否则不符合条件舍掉。在求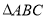 面积时若采用先求弦
面积时若采用先求弦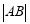 再求点
再求点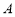 到
到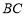 的距离最后求面积的方法计算过于繁琐,所以求
的距离最后求面积的方法计算过于繁琐,所以求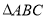 的面积时可用分割法,计算较简单。
的面积时可用分割法,计算较简单。
试题解析:【解析】
(Ⅰ)由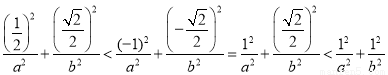 知,
知,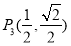 和
和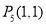 不在椭圆
不在椭圆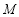 上,即椭圆
上,即椭圆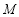 经过
经过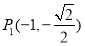 ,
,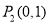 ,
, .
.
于是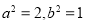 .
.
所以 椭圆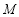 的方程为:
的方程为: . 2分
. 2分
(Ⅱ)①当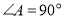 时,设直线
时,设直线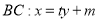 ,由
,由 得
得
 .设
.设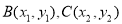 ,则
,则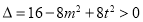 ,
,
所以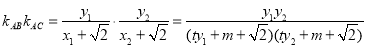

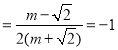 .
.
于是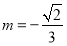 ,此时
,此时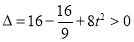 ,所以 直线
,所以 直线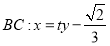 .
.
因为 ,故线段
,故线段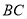 与
与 轴相交于
轴相交于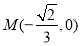 ,即原点在线段
,即原点在线段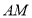 的延长线上,即原点在
的延长线上,即原点在 的外部,符合题设. 6分
的外部,符合题设. 6分
所以 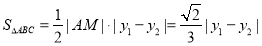
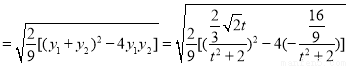
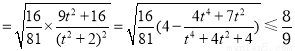 .
.
当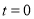 时取到最大值
时取到最大值 . 9分
. 9分
②当 时,不妨设
时,不妨设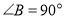 .
.
设直线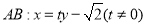 ,由
,由 得
得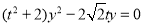 .
.
所以 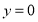 或
或 .
.
所以 ,由
,由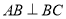 ,可得直线
,可得直线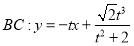 .
.
由 得
得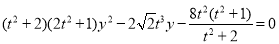 .
.
所以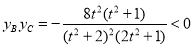 .
.
所以线段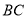 与
与 轴相交于
轴相交于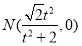 .
.
显然原点在线段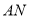 上,即原点在
上,即原点在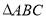 的内部,不符合题设.
的内部,不符合题设.
综上所述,所求的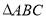 面积的最大值为
面积的最大值为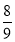 . 12分
. 12分
考点:1、椭圆的对称性和方程;2、直线和椭圆的位置关系问题;3、三角形面积的求法。

练习册系列答案
相关题目