题目内容
抛物线
的准线方程是 ( )
（A） 
（B）
（C）
（D）
C
【解析】
试题分析：由抛物线方程可知，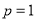
，焦点在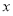
轴正半轴，所以其准线方程为
。故C正确。
考点：抛物线准线方程。
练习册系列答案
相关题目
题目内容
抛物线的准线方程是 ( )
（A） （B） （C） （D）
C
【解析】
试题分析：由抛物线方程可知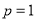，，焦点在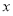轴正半轴，所以其准线方程为。故C正确。
考点：抛物线准线方程。
