题目内容
在△ABC中,CD是AB边上的高,a,b和c为三边,且c最长,
+
=1,则( )
| CD2 |
| AC2 |
| CD2 |
| BC2 |
A、A+B=
| ||
B、A-B=
| ||
C、B-A=
| ||
D、|A-B|=
|
分析:先分别求得
=sinA,
=sinB,进而根据题意求得sin2A+sin2B=1,同时,利用二倍角公式可知sin2A+sin2B=
(1-cos2A+1-cos2B)整理求得cos(A-B)cos(A+B)=0,根据c边最长,可知A<
,进而推断出A+B=
.
| CD |
| AC |
| CD |
| BC |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
解答:解:在Rt△ACD中
=sinA,
=sinB
∵
+
=1
∴sin2A+sin2B=1
∵sin2A+sin2B=
(1-cos2A+1-cos2B)=1-cos(A-B)cos(A+B)=1
cos(A-B)cos(A+B)=0
A-B=
或者A+B=
由c边最长,知C最大,那么A<
,只能是A+B=
故选A.
| CD |
| AC |
| CD |
| BC |
∵
| CD2 |
| AC2 |
| CD2 |
| BC2 |
∴sin2A+sin2B=1
∵sin2A+sin2B=
| 1 |
| 2 |
cos(A-B)cos(A+B)=0
A-B=
| π |
| 2 |
| π |
| 2 |
由c边最长,知C最大,那么A<
| π |
| 2 |
| π |
| 2 |
故选A.
点评:本题主要考查了解三角形的问题.考查了学生综合分析问题和推理的能力.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
在△ABC中,CD是AB边上的高,a2+c2<b2,
+
=1,则( )
| CD2 |
| AC2 |
| CD2 |
| BC2 |
A、A+B=
| ||
B、A-B=
| ||
C、B-A=
| ||
D、|A-B|=
|
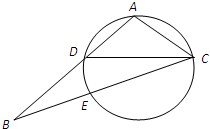 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AB=2AC,
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AB=2AC, 选考题
选考题