题目内容
在△ABC中,CD是AB边上的高,a2+c2<b2,
+
=1,则( )
| CD2 |
| AC2 |
| CD2 |
| BC2 |
A、A+B=
| ||
B、A-B=
| ||
C、B-A=
| ||
D、|A-B|=
|
分析:在△ABC中,a2+c2<b2由余弦定理可得∠B为钝角,由
+
=1可得sin2A+sin2B=1,继而得sin(π-B)=sin(
-A),由条件可判断π-B,
-A均为锐角,问题即可解决.
| CD2 |
| AC2 |
| CD2 |
| BC2 |
| π |
| 2 |
| π |
| 2 |
解答:解:由余弦定理得cosB=
<0,则90°<B<180°;
在Rt△BCD中,sin(π-B)=sinB=
,
在Rt△ACD中,sinA=
;又
+
=1,
又sin2A+sin2B=1,移项得sin2A=cos2B,又B∈(
,π),
∴sin(π-B)=cosA=sin(
-A),得B-A=
,
故选C.
| a2+c2-b2 |
| 2ac |
在Rt△BCD中,sin(π-B)=sinB=
| CD |
| BC |
在Rt△ACD中,sinA=
| CD |
| AC |
| CD2 |
| AC2 |
| CD2 |
| BC2 |
又sin2A+sin2B=1,移项得sin2A=cos2B,又B∈(
| π |
| 2 |
∴sin(π-B)=cosA=sin(
| π |
| 2 |
| π |
| 2 |
故选C.
点评:本题考查解三角形及三角恒等变换.解决的关键在于对条件
+
=1的转化与应用,考查了学生综合分析与应用三角函数公式的能力.
| CD2 |
| AC2 |
| CD2 |
| BC2 |

练习册系列答案
相关题目
在△ABC中,CD是AB边上的高,a,b和c为三边,且c最长,
+
=1,则( )
| CD2 |
| AC2 |
| CD2 |
| BC2 |
A、A+B=
| ||
B、A-B=
| ||
C、B-A=
| ||
D、|A-B|=
|
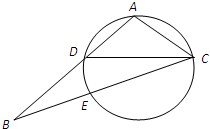 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AB=2AC,
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AB=2AC, 选考题
选考题