[题目]将....这5名同学从左至右排成一排.则与相邻且与之间恰好有1名同学的排法有种. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】将，，，，这5名同学从左至右排成一排，则与相邻且与之间恰好有1名同学的排法有________种.

【答案】20

【解析】

由与相邻且与之间恰好有1名同学，分类讨论B在A与C之间，与B在A的另一侧，A与C之间为D，E中任意1人两种情况，分类计数之后再相加得答案.

根据题意，分两种情况

若A与C之间为B，即B在A,C中间且三人相邻，共有种情况，

将三人看成一个整体，与D,E两人全排列，共有种情况，

则此时有种排法

若A与C之间不是B，先从D，E中选取1人，安排在A，C之间，有种选法，

此时B在A的另一侧，将四人看成一个整体，考虑之前的顺序，有种情况，

将这个整体与剩下的1人全排列，有种情况，

此时有种排法

所以总共有种情况符合题意

故答案为：20

练习册系列答案

	常喝	不常喝	总计
肥胖		2
不肥胖		18
总计			30

已知从这30名青少年中随机抽取1名，抽到肥胖青少年的概率为．

（1）请将列联表补充完整；（2）是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关？

独立性检验临界值表：

P（K2≥k0）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k0	2.072	2.706	3.841	5.024	6.635	7.879	10.828

参考公式：，其中n=a+b+c+d．

【题目】已知抛物线，其焦点到准线的距离为2，直线与抛物线交于，两点，过，分别作抛物线的切线，，与交于点.

（Ⅰ）求的值；

（Ⅱ）若，求面积的最小值.

【题目】已知函数

(1)判断函数在上的单调性

(2)若恒成立，求整数的最大值

(3)求证：

【题目】在中老年人群体中，肠胃病是一种高发性疾病某医学小组为了解肠胃病与运动之间的联系，调查了50位中老年人每周运动的总时长（单位：小时），将数据分成[0，4），[4，8），[8，14），[14，16），[16，20），[20，24]6组进行统计，并绘制出如图所示的柱形图．

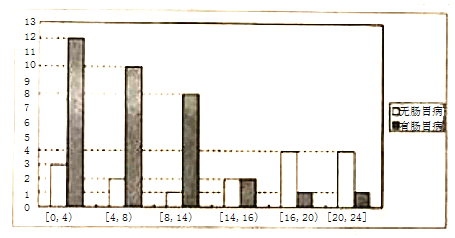
图中纵轴的数字表示对应区间的人数现规定：每周运动的总时长少于14小时为运动较少．

每周运动的总时长不少于14小时为运动较多．

（1）根据题意，完成下面的2×2列联表：

	有肠胃病	无肠胃病	总计
运动较多
运动较少
总计

（2）能否有99.9%的把握认为中老年人是否有肠胃病与运动有关？

附：K2（n＝a+b+c+d）

P（K2≥k）	0.0.50	0.010	0.001
k	3.841	6.635	10.828

【题目】已知数列满足：，，设数列的前项和为.证明：

（Ⅰ）；

（Ⅱ）；

（Ⅲ）.

【题目】已知两点分别在轴和轴上运动，且，若动点满足.

（1）求出动点P的轨迹对应曲线C的标准方程；

（2）一条纵截距为2的直线与曲线C交于P，Q两点，若以PQ直径的圆恰过原点，求出直线方程.

【题目】设函数，若方程在区间内有个不同的实数解，则实数的取值范围为_____．

【题目】已知点是椭圆C：上的一点，椭圆C的离心率与双曲线的离心率互为倒数，斜率为直线l交椭圆C于B，D两点，且A、B、D三点互不重合．

（1）求椭圆C的方程；

（2）若分别为直线AB，AD的斜率，求证：为定值。

试题分类