题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c.若acosA=bsinB,则sinAcosA+cos2B等于( )
A.-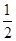 | B.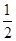 | C.-1 | D.1 |
D
因为在△ABC中,acosA=bsinB,
由正弦定理可得sinAcosA=sin2B,
即sinAcosA=1-cos2B,
所以sinAcosA+cos2B=1.故选D.
由正弦定理可得sinAcosA=sin2B,
即sinAcosA=1-cos2B,
所以sinAcosA+cos2B=1.故选D.

练习册系列答案
相关题目
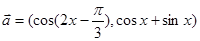 ,
,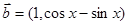 ,函数
,函数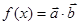 .
.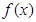 的单调递增区间;
的单调递增区间;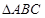 中,内角
中,内角 的对边分别为
的对边分别为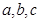 ,已知
,已知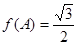 ,
,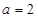 ,
,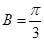 ,求
,求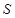 .
. 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知 ,
,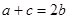 ;
; ,求
,求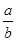 的值.
的值.
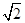 (B)2
(B)2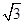 (C)
(C)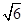 -
-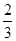 .
.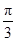 )的值.
)的值.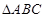 中,已知
中,已知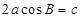 ,
,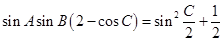 ,则
,则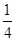 ,b=2,sin C=2sin A,则△ABC的面积为( ).
,b=2,sin C=2sin A,则△ABC的面积为( ).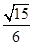
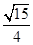
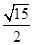
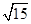
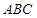 中,三个内角
中,三个内角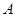 ,
,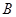 ,
,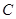 所对的边分别为
所对的边分别为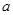 ,
,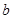 ,
,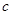 ,若
,若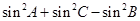
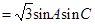 ,则
,则