题目内容
已知直线l上有一列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,其中n∈N*,x1=1,x2=2,点Pn+2分有向线段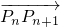 所成的比为λ(λ≠-1).
所成的比为λ(λ≠-1).
(1)写出xn+2与xn+1,xn之间的关系式;
(2)设an=xn+1-xn,求数列{an}的通项公式.
解:(1)因为点Pn+2分有向线段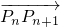 所成的比为λ,
所成的比为λ,
所以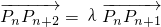 ,即由定比分点坐标公式得xn+2=
,即由定比分点坐标公式得xn+2=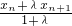 .
.
(2)a1=x2-x1=1,
因为an+1=xn+2-xn+1=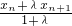 -xn+1
-xn+1
=-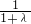 (xn+1-xn)=-
(xn+1-xn)=-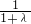 an,
an,
∴ =-
=-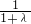 ,即{an}是以a1=1为首项,-
,即{an}是以a1=1为首项,-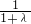 为公比的等比数列.
为公比的等比数列.
∴an=(-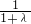 )n-1.
)n-1.
分析:(1)直接利用向量的定比分点坐标公式写出xn+2与xn+1,xn之间的关系式;
(2)由an=xn+1-xn,求出a1,再推出an和an+1的关系,说明是等比数列,然后求数列{an}的通项公式.
点评:本题考查线段的定比分点,数列递推式,考查转化思想,考查逻辑思维能力,是中档题.
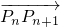 所成的比为λ,
所成的比为λ,所以
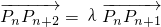 ,即由定比分点坐标公式得xn+2=
,即由定比分点坐标公式得xn+2=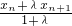 .
.(2)a1=x2-x1=1,
因为an+1=xn+2-xn+1=
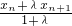 -xn+1
-xn+1=-
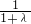 (xn+1-xn)=-
(xn+1-xn)=-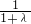 an,
an,∴
 =-
=-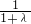 ,即{an}是以a1=1为首项,-
,即{an}是以a1=1为首项,-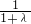 为公比的等比数列.
为公比的等比数列.∴an=(-
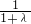 )n-1.
)n-1.分析:(1)直接利用向量的定比分点坐标公式写出xn+2与xn+1,xn之间的关系式;
(2)由an=xn+1-xn,求出a1,再推出an和an+1的关系,说明是等比数列,然后求数列{an}的通项公式.
点评:本题考查线段的定比分点,数列递推式,考查转化思想,考查逻辑思维能力,是中档题.

练习册系列答案
相关题目
 中n∈N*,x1=1,x2=2,点Pn+2分有向线段
中n∈N*,x1=1,x2=2,点Pn+2分有向线段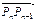 所成的比为λ(λ≠-1).
所成的比为λ(λ≠-1). 所成的比为λ(λ≠-1).
所成的比为λ(λ≠-1).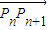 所成的比为λ(λ≠-1).
所成的比为λ(λ≠-1).