题目内容
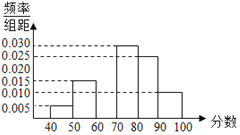
【题目】某校![]() 名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是
名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
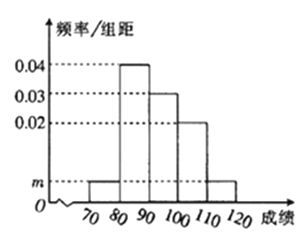
![]() 求图中
求图中![]() 的值;
的值;
![]() 根据频率分布直方图,估计这
根据频率分布直方图,估计这![]() 名学生的平均分;
名学生的平均分;
![]() 若这
若这![]() 名学生的数学成绩中,某些分数段的人数
名学生的数学成绩中,某些分数段的人数![]() 与英语成绩相应分数段的人数
与英语成绩相应分数段的人数![]() 之比如表所示,求英语成绩在
之比如表所示,求英语成绩在![]() 的人数.
的人数.
分数段 |
|
|
|
|
| 1:2 | 1:1 |
【答案】(1)![]() (2)平均数为
(2)平均数为![]() (3)
(3)![]() 人
人
【解析】
(1)根据面积之和为1列等式解得.
(2)频率分布直方图中每一个小矩形的面积乘以底边中点的横坐标之和即为平均数,
(3)先计算出各分数段上的成绩,再根据比值计算出相应分数段上的英语成绩人数相加即可.
解:![]() 由
由![]() ,
,
解得![]() .
.
![]() 频率分布直方图中每一个小矩形的面积乘以底边中点的横坐标之和即为平均数,
频率分布直方图中每一个小矩形的面积乘以底边中点的横坐标之和即为平均数,
即估计平均数为![]() .
.
![]() 由频率分布直方图可求出这
由频率分布直方图可求出这![]() 名学生的数学成绩在
名学生的数学成绩在![]() ,
,![]() ,
,![]() 的分别有
的分别有![]() 人,
人,![]() 人,
人,![]() 人,按照表中给的比例,则英语成绩在
人,按照表中给的比例,则英语成绩在![]() ,
,![]() ,
,![]() 的分别有
的分别有![]() 人,
人,![]() 人,
人,![]() 人,所以英语成绩在
人,所以英语成绩在![]() 的有
的有![]() 人.
人.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
【题目】历史数据显示:某城市在每年的3月11日—3月15日的每天平均气温只可能是-5℃,-6℃,-7℃,-8℃中的一个,且等可能出现.
(Ⅰ)求该城市在3月11日—3月15日这5天中,恰好出现两次-5℃,一次-8℃的概率;
(Ⅱ)若该城市的某热饮店,随平均气温的变化所售热饮杯数如下表
平均气温t | -5℃ | -6℃ | -7℃ | -8℃ |
所售杯数y | 19 | 22 | 24 | 27 |
根据以上数据,求![]() 关于
关于![]() 的线性回归直线方程.
的线性回归直线方程.
(参考公式: ,
,![]() )
)