题目内容
【题目】已知椭圆![]() :
:![]() 的上顶点为
的上顶点为![]() ,右焦点为F,连结TF并延长与椭圆
,右焦点为F,连结TF并延长与椭圆![]() 交于点S,且
交于点S,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与x轴交于点M,过点M的直线AB与
与x轴交于点M,过点M的直线AB与![]() 交于A、B两点,点P为直线
交于A、B两点,点P为直线![]() 上任意一点,设直线AB与直线
上任意一点,设直线AB与直线![]() 交于点N,记PA,PB,PN的斜率分别为
交于点N,记PA,PB,PN的斜率分别为![]() ,
,![]() ,
,![]() ,则是否存在实数
,则是否存在实数![]() ,使得
,使得![]() 恒成立?若是,请求出
恒成立?若是,请求出![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在, ![]()
【解析】
(1)易得![]() ,由连结TF并延长与椭圆
,由连结TF并延长与椭圆![]() 交于点S,且
交于点S,且![]() ,可得
,可得![]() ,代入椭圆方程可得
,代入椭圆方程可得![]() ,可得椭圆方程;
,可得椭圆方程;
(2)可得M点坐标![]() ,设直线AB的方程为:
,设直线AB的方程为:![]() ,设
,设![]() ,
,![]() ,,可得N点坐标
,,可得N点坐标![]() ,设P点坐标
,设P点坐标![]() ,可得
,可得![]() ,联立直线与椭圆方程,可得
,联立直线与椭圆方程,可得![]() ,
,![]() 的值,
的值,![]() ,计算
,计算![]() 的值,代入
的值,代入![]() ,
,![]() ,与
,与![]() 进行比较可得
进行比较可得![]() 的值.
的值.
解:由椭圆![]() :
:![]() 的上顶点为
的上顶点为![]() ,可得
,可得![]() ,
,
连结TF并延长与椭圆![]() 交于点S,且
交于点S,且![]() ,可得
,可得![]() ,
,
代入椭圆方程:![]() ,可得
,可得![]() ,可得
,可得![]() ,结合
,结合![]() ,
,
可得![]() ,
,![]() ,故椭圆方程为:
,故椭圆方程为:![]() ;
;
(2)可得M点坐标![]() ,设直线AB的方程为:
,设直线AB的方程为:![]() ,
,
设![]() ,
,![]() ,可得N点坐标
,可得N点坐标![]() ,
,
设P点坐标![]() ,可得
,可得![]() ,
,
联立直线与椭圆方程可得: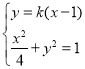 ,化简可得:
,化简可得:![]() ,
,
可得:![]() ,
,![]() ,
,
可得:![]() ,
,![]() ,
,
可得![]() ,
,
代入:![]() ,
,![]() ,
,
可得: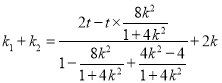 ,化简可得
,化简可得![]() ,
,
由![]() 恒成立,可得
恒成立,可得![]() ,
,
可得当![]() 时
时![]() 恒成立.
恒成立.

【题目】某部门在十一月份对城市居民进行了主题为空气质量问卷调查,根据每份调查表得到每个调查对象的空气质量评分值(百分制).现从收到的调查表中随机抽取20份进行统计,得到如图所示的频率分布表:
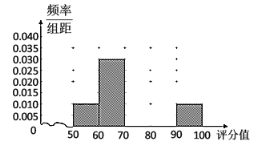
空气质量评分值 | 频数 | 频率 |
[50,60] | 2 |
|
(60.70] | 6 |
|
(70,80] |
|
|
(80,90] | 3 |
|
(90,100] | 2 |
|
(1)请完成题目中的频率分布表,并补全题目中的频率分布直方图;
(2)该部门将邀请被问卷调查的部分居民参加如何提高空气质量的座谈会.在题中抽样统计的这20人中,已知空气质量评分值在区间(80,100]的5人中有2人被邀请参加座谈,求其中幸福指数评分值在区间(80,90]的仅有1人被邀请的概率.
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
18 | |||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: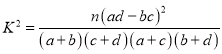 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |