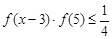题目内容
若非零函数 对任意实数
对任意实数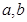 均有
均有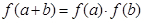 ,且当
,且当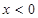 时,
时,
 ;
;
(1)求证: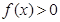 (2)求证:
(2)求证: 为减函数
为减函数
(3)当 时,解不等式
时,解不等式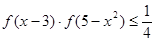
【答案】
(1)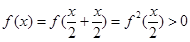 ;
;
(2)见解析;(3)不等式的解集为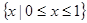 。
。
【解析】
试题分析:(1)利用已知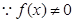

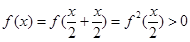 ,可得结论。
,可得结论。
(2)根据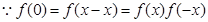 =1,得到f(x)与f(-x)的关系式,进而求解得到。
=1,得到f(x)与f(-x)的关系式,进而求解得到。
(3)由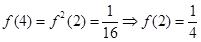 原不等式转化为
原不等式转化为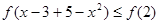 进而结合单调性得到。
进而结合单调性得到。
解:(1)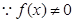

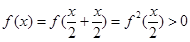 ------------3分
------------3分
(2)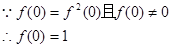 -------------5分
-------------5分
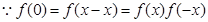
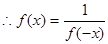 -------------8分
-------------8分
设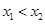 则
则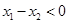
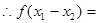
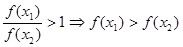 ,
,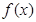 为减函数
为减函数
-------10分
(3)由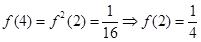 原不等式转化为
原不等式转化为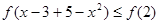 ,结合(2)得:
,结合(2)得: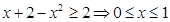
故不等式的解集为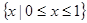 ------------------13分
------------------13分
考点:本题主要考查了函数的性质以及不等式的求解的运用。
点评:解决该试题的关键是抽象函数的赋值法思想的运用,判定单调性和f(x)与f(-x)的关系式的运用。

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
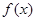 对任意实数
对任意实数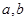 均有¦(a+b)=¦(a)·¦(b),且当
均有¦(a+b)=¦(a)·¦(b),且当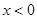 时,
时,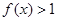 .
. 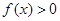 ;
; 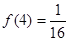 时,解不等式
时,解不等式
 对任意实数
对任意实数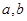 均有¦(a+b)=¦(a)·¦(b),且当
均有¦(a+b)=¦(a)·¦(b),且当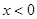 时,
时, .
.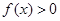
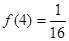 时,解不等式
时,解不等式