题目内容
已知 是函数
是函数 的导数,则
的导数,则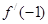 =
=
6
解析试题分析:因为 ,所以
,所以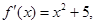 因此
因此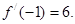 初步学习导数要注意
初步学习导数要注意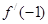 是导函数在
是导函数在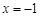 处的函数值,而不是
处的函数值,而不是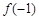 的导数.
的导数.
考点:函数的导数

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
题目内容
已知 是函数
是函数 的导数,则
的导数,则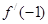 =
=
6
解析试题分析:因为 ,所以
,所以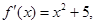 因此
因此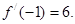 初步学习导数要注意
初步学习导数要注意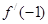 是导函数在
是导函数在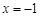 处的函数值,而不是
处的函数值,而不是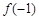 的导数.
的导数.
考点:函数的导数

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案