题目内容
【题目】在斜三棱柱ABC﹣A1B1C1中,底面ABC是正三角形,E是AB中点,A1E⊥平面ABC.
(I)证明:BC1∥平面 A1EC;
(II)若A1A⊥A1B,且AB=2.
①求点B到平面ACC1A1的距离;
②求直线CB1与平面ACC1A1所成角的正弦值.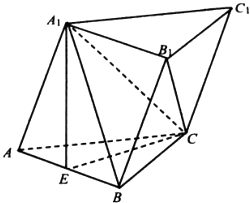
【答案】解:(I)证明:设AC1与A1C交于F点,连接EF,
∵E,F分别是线段AB,AC1的中点,
∴EF∥BC1 , 又EF平面 A1EC,BC1平面A1EC
故 BC1∥平面A1EC,
(II)①在正三角形A BC中,过E作E H⊥AC于H,连接A1H
显然AC⊥平面A1EH,
∵AC平面ACC1A1
∴平面A1EH⊥平面ACC1A1 , 且两个平面的交线为A1H
过E作EG⊥A1H于G,则EG⊥平面ACC1A1
在Rt△AA1B中,由已知易得A1E=1,在正三角形ABC中, ![]()
则在Rt△A1E H中, 
即点E到平面ACC1A1的距离为 ![]() ,
,
∵E是线段AB中点,
∴点B到平面ACC1A1的距离 ![]() ,
,
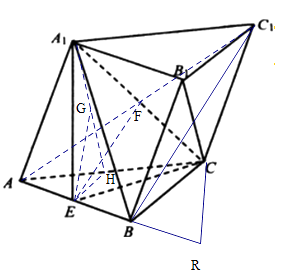
②延长EB至R点,使EB=BR=1,连接RC,
∴B1R∥A1E,则B1R⊥平面ARC,即有B1R⊥RC
在△BRC中易得 ![]() ,
,
∴ ![]()
设直线B1C与平面ACC1A1所成角为φ
则 ![]() .
.
【解析】(Ⅰ)根据线面平行的判定定理进行证明即可.(Ⅱ)根据点到平面的距离公式以及线面角的定义,结合三角形的边角关系进行求解.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则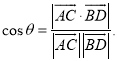 .
.

练习册系列答案
相关题目


