题目内容
(1)已知复数z=| (1-4i)(1+i)+2+4i |
| 3+4i |
(2)已知z2=8+6i,求z+
| 100 |
| z |
分析:(1)求出z=1-i,代入z2+az+b=1+i,得:a+b-(a+2)=1+i,利用两个复数相等的充要条件求出实数a、b的值.
(2)设z=x+yi(x、y∈R),代入z2=8+6i,解得
或
,从而得到得到复数z的值.
(2)设z=x+yi(x、y∈R),代入z2=8+6i,解得
|
|
解答:解:(1)z=
=
=1-i,代入z2+az+b=1+i,得:a+b-(a+2)=1+i,
所以有
,解得
.
(2)设z=x+yi(x、y∈R),代入z2=8+6i得:(x+yi)2=8+6i,所以有(x2-y2)+2xy=8+6i,
从而得方程组
,解得
或
.
①当
时,原式=z(1+
)=z(1+8-6i)=(3+i)(9-6i)=33-9i;
②当
时,原式=z(1+
)=z(1+8-6i)=-(3+i)(9-6i)=-33+9i.
综上所述,z+
的值是±(33-9i).
| 7+i |
| 3+4i |
| (7+i)(3-4i) |
| 25 |
所以有
|
|
(2)设z=x+yi(x、y∈R),代入z2=8+6i得:(x+yi)2=8+6i,所以有(x2-y2)+2xy=8+6i,
从而得方程组
|
|
|
①当
|
| 100 |
| z2 |
②当
|
| 100 |
| z2 |
综上所述,z+
| 100 |
| z |
点评:本题考查复数的基本概念,复数代数形式的混合运算,两个复数相等的充要条件,求出复数z,是解题的关键.

练习册系列答案
相关题目
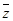 及|
及|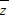 及|
及|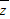 |;
|;