题目内容
(1)已知复数z满足z•
=2iz=4+2i,求复数z.
(2)解关于x的不等式
>0(a∈R).
| z |
(2)解关于x的不等式
| x-a2 |
| a-x |
分析:(1)设出复数的代数形式,利用两个复数的乘法法则和两个复数相等的条件建立方程组,用待定系数法求复数.
(2)把不等式
>0(a∈R)转化为同解不等式,对a分类讨论解答即可.
(2)把不等式
| x-a2 |
| a-x |
解答:解:(1)设z=x+yi,x,y∈R,则
=x-yi.
由题意,得(x+yi)(x-yi)+2(x+yi)i=(x2+y2-2y)+2xi=4+2i.
由复数相等的条件得出的方程组
,
故解得
或
∴z=1+3i或z=1-i
(2)不等式等价于(x-a2)(x-a)<0,
若a=0,则x2<0,
所以x∈∅
若a=1,则(x-1)2<0,
所以x∈∅
若a<0,或a>1,则a<a2,
所以x∈(a,a2)
若0<a<1,则a2<a,
所以x∈(a2,a).
| z |
由题意,得(x+yi)(x-yi)+2(x+yi)i=(x2+y2-2y)+2xi=4+2i.
由复数相等的条件得出的方程组
|
故解得
|
|
∴z=1+3i或z=1-i
(2)不等式等价于(x-a2)(x-a)<0,
若a=0,则x2<0,
所以x∈∅
若a=1,则(x-1)2<0,
所以x∈∅
若a<0,或a>1,则a<a2,
所以x∈(a,a2)
若0<a<1,则a2<a,
所以x∈(a2,a).
点评:(1)本小题考查两个复数代数形式的乘除法,共轭复数的概念,两个复数相等的条件.
(2)本小题考查含有字母变量的不等式的解法,考查分类讨论思想,是中档题.
(2)本小题考查含有字母变量的不等式的解法,考查分类讨论思想,是中档题.

练习册系列答案
相关题目
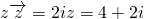 ,求复数z.
,求复数z.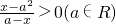 .
.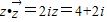 ,求复数z.
,求复数z.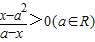 .
. ,求复数z.
,求复数z.
 的展开式中,第5项的系数与第3项的系数之比是56:3,求展开式中的常数项。
的展开式中,第5项的系数与第3项的系数之比是56:3,求展开式中的常数项。