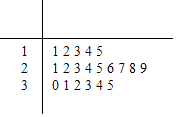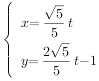��Ŀ����
����Ŀ�����ں���f1��x����f2��x����h��x�����������ʵ��a��bʹ��h��x��=af1��x��+bf2��x������ô��h��x��Ϊf1��x����f2��x�������ɺ�����
��1���������� ![]() ��h��x���Ƿ�Ϊf1��x���� f2��x�������ɺ�������˵�����ɣ�
��h��x���Ƿ�Ϊf1��x���� f2��x�������ɺ�������˵�����ɣ�
��2���� ![]() �����ɺ���h��x����������ʽ3h2��x��+2h��x��+t��0��x��[2��4]�Ϻ��������ʵ��t��ȡֵ��Χ��
�����ɺ���h��x����������ʽ3h2��x��+2h��x��+t��0��x��[2��4]�Ϻ��������ʵ��t��ȡֵ��Χ��
��3���� ![]() ��ȡa��0��b��0�����ɺ���h��x��ͼ�����͵�����Ϊ��2��8����������������ʵ��x1 �� x2��x1+x2=1�������Ƿ�������ij���m��ʹh��x1��h��x2����m�������������ڣ�������m��ֵ����������ڣ���˵�����ɣ�
��ȡa��0��b��0�����ɺ���h��x��ͼ�����͵�����Ϊ��2��8����������������ʵ��x1 �� x2��x1+x2=1�������Ƿ�������ij���m��ʹh��x1��h��x2����m�������������ڣ�������m��ֵ����������ڣ���˵�����ɣ�
���𰸡�
��1���⣺���� ![]() ��
��
��h��x����af1��x��+bf2��x�������ɺ�����
����lgx= ![]() ��
��
�ɣ� ![]() ����ã�
����ã� ![]() ������ʵ��a��b�������⣮
������ʵ��a��b�������⣮
��h��x����f1��x����f2��x�������ɺ�����
��2���⣺�����⣬ ![]() �����ɺ���h��x����
�����ɺ���h��x����
��h��x��=2f1��x��+f2��x��= ![]()
��h��x���Ƕ������ڵ���������
��3h2��x��+2h��x��+t��0��x��[2��4]�Ϻ������
�� ![]() ��
��
��S=log2x����S��[1��2]��
��ô�У�y=��3S2��2S��
��Գ���S= ![]() ��
��
�ੁ16��y�ܩ�5��
�ʵ�t����5��
��3���⣺�����⣬��h��x��=af1��x��+bf2��x��=ax ![]() ��
��
��h��x��=ax ![]() ��2
��2 ![]()
�� 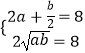 ����ã�a=2��b=8��
����ã�a=2��b=8��
��h��x��=2x+ ![]() ����x��0��
����x��0��
�������ij���m��ʹh��x1��h��x2����m�������
��u=h��x1��h��x2��= ![]()
![]() =
= ![]()
��x1+x2=1��
��u= ![]() ��
��
��t=x1x2����t=x1x2�� ![]() ����
���� ![]() ��
��
��ô��u=4t ![]() ����
���� ![]() ���ǵ����ݼ���
���ǵ����ݼ���
��u��u�� ![]() ��=289��
��=289��
�����ij���m=289��
����������1�������¶���h��x��=af1��x��+bf2��x���жϼ��ɣ���2�������¶������ɺ���h��x�������������䵥���ԣ����û�Ԫ��ת��Ϊ���κ������������ֵ���������������⣮��3�������¶������ɺ���h��x�������û�������ʽ�����ɺ���h��x��ͼ�����͵�����Ϊ��2��8��������ab���������ij���m��ʹh��x1��h��x2����m����������뻯�����û�Ԫ�����������ʽ�ж������ֵ�Ƿ���ڼ�����⣮