题目内容
已知定点A (2,0),点P是圆x2+y2=1上的动点,且∠AOP的平分线交AP于M,当P在圆上运动时,求动点M的轨迹方程。
解:设动点P(cosθ, sinθ),
直线OM:y=tan x,
x,
直线PA:y= (x-2),
(x-2),
由OM的方程可得tan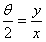 (x≠0),
(x≠0),
代入PA的方程得 ,
,
化简,可得动点M的轨迹方程为(x-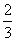 )2+y2=
)2+y2=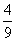 (y≠0)。
(y≠0)。
直线OM:y=tan
 x,
x,直线PA:y=
 (x-2),
(x-2),由OM的方程可得tan
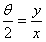 (x≠0),
(x≠0),代入PA的方程得
 ,
,化简,可得动点M的轨迹方程为(x-
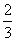 )2+y2=
)2+y2=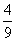 (y≠0)。
(y≠0)。 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
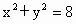 ,动点M在圆O上,那么∠OMA的最大值是
,动点M在圆O上,那么∠OMA的最大值是
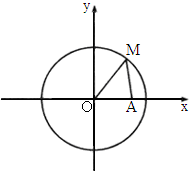
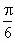
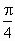
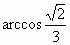
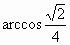

 ,设动点M的轨迹为曲线C.
,设动点M的轨迹为曲线C. 与曲线C交于P,Q两点,若
与曲线C交于P,Q两点,若 ,证明:
,证明: 为定值.
为定值.