题目内容
【题目】已知过定点![]() 且与直线
且与直线![]() 垂直的直线与
垂直的直线与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,点
,点 满足
满足![]() .
.
(1)若以原点为圆心的圆![]() 与
与![]() 有唯一公共点,求圆
有唯一公共点,求圆![]() 的轨迹方程;
的轨迹方程;
(2)求能覆盖![]() 的最小圆的面积;
的最小圆的面积;
(3)在(1)的条件下,点![]() 在直线
在直线![]() 上,圆
上,圆![]() 上总存在两个不同的点
上总存在两个不同的点![]() 使得
使得![]()
![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)![]() ,得
,得![]() 在直线
在直线![]() 上,求出
上,求出![]() ,确定圆的半径则方程可求
,确定圆的半径则方程可求
(2)由几何关系得能覆盖三角形ABC的最小圆是以AB为直径的圆,计算![]() ,则圆的面积可求
,则圆的面积可求
(3)由![]() ,则有OP与MN互相垂直平分,得
,则有OP与MN互相垂直平分,得![]() 利用点在直线上得
利用点在直线上得![]() 的不等式求解
的不等式求解
(1)因为![]() ,所以
,所以![]() 在线段
在线段![]() 的垂直平分线上,即在直线
的垂直平分线上,即在直线![]() 上,
上,
故![]()
以原点为圆心的圆![]() 与
与![]() 有唯一公共点,
有唯一公共点,
此时圆的半径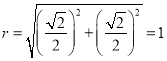
故:圆![]() 的方程为
的方程为![]()
(2)由于三角形ABC为钝角三角形且AB为最长边,故能覆盖三角形ABC的最小圆是以AB为直径的圆
由于点![]() ,所以
,所以![]()
故该圆的半径为![]()
所以能覆盖该三角形的最小圆面积![]()
(3)![]() span>(O为坐标原点),则有OP与MN互相垂直平分,
span>(O为坐标原点),则有OP与MN互相垂直平分,
所以圆心到直线MN的距离小于1.即又![]()
又![]() ,代入(1)得
,代入(1)得
![]()
所以实数![]() 的取值范围为
的取值范围为![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目