题目内容
【题目】已知函数f(x)=(x+1)lnx,g(x)=a(x﹣1)(a∈R).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)≥g(x)对任意的x∈[1,+∞)恒成立,求实数a的取值范围;
(Ⅲ)求证:ln2ln3…lnn> ![]() (n≥2,n∈N+).
(n≥2,n∈N+).
【答案】解:(Ⅰ)f(x)的定义域为(0,+∞),f′(x)=lnx+ ![]() +1,
+1,
设g(x)=f′(x),g′(x)= ![]() ,
,
令g′(x)>0,得x>1,g′(x)<0,得0<x<1,
∴g(x)在(0,1)递减,在(1,+∞)递增,g(x)min=g(1)=2,
∴f′(x)>0在(0,+∞)上恒成立,
∴f(x)的递增区间为(0,+∞),无递减区间.
(Ⅱ)设h(x)=(x﹣1)lnx﹣ax+a,
由(Ⅰ)知:h′(x)=lnx+ ![]() =1﹣a=g(x)﹣a,
=1﹣a=g(x)﹣a,
g(x)在(1,+∞)递增,∴g(x)≥g(1)=2,
(i)当a≤2时,h′(x)≥0,h(x)在[1,+∞)递增,
∴h(x)≥h(1)=0,满足题意.
(ii)当a>2时,设ω(x)=h′(x),ω′(x)= ![]() ,
,
当x≥1时,ω′(x)≥0,∴ω(x)在[1,+∞)递增,
ω(1)=2﹣a<0,ω(ea)=1+e﹣a>0,
∴x0∈(1,ea),使ω(x0)=0,∵ω(x)在[1,+∞)递增,
∴x∈(1,x0),ω(x)<0,即h′(x)<0,
∴当x∈(1,x0时,h(x)<h(1)=0,不满足题意.
综上,a的取值范围为(﹣∞,2].
(Ⅲ)由(Ⅱ)知,令a=2,(x+1)lnx≥2(x﹣1),
∴x≥1,lnx≥ ![]() (当且仅当x=1取“=”),
(当且仅当x=1取“=”),
令x=n(n≥2,n∈N*)得lnn> ![]() ,
,
即ln2> ![]() ,ln3>
,ln3> ![]() ,ln4>
,ln4> ![]() ,…,
,…,
ln(n﹣2)> ![]() ,ln(n﹣1)>
,ln(n﹣1)> ![]() ,lnn>
,lnn> ![]() ,
,
将上述n﹣1个式子相乘得:ln2ln3…lnn> 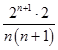 =
= 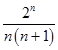 ,
,
∴原命题得证
【解析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(Ⅱ)求出h(x)的导数,通过讨论a的范围,结合函数的单调性确定a的具体范围即可;(Ⅲ)得到lnx≥ ![]() ,令x=n(n≥2,n∈N*),得lnn>
,令x=n(n≥2,n∈N*),得lnn> ![]() ,x取不同的值,相乘即可.
,x取不同的值,相乘即可.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】某保险的基本保费为a(单位:元),继续购买该保险的投保人成为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(Ⅰ)求一续保人本年度的保费高于基本保费的概率;
(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(Ⅲ)求续保人本年度的平均保费与基本保费的比值.

