题目内容
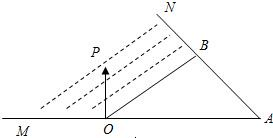 如图,在△OAB中,点P是线段OB及AB、AO的延长线所围成的阴影区域内(含边界)的任意一点,且
如图,在△OAB中,点P是线段OB及AB、AO的延长线所围成的阴影区域内(含边界)的任意一点,且| OP |
| OA |
| OB |
A、
| ||
B、
| ||
| C、4 | ||
| D、5 |
分析:通过点P是线段OB及AB、AO的延长线所围成的阴影区域内(含边界)的任意一点,作OB的平行线,把
=x
+y
,中的x,y表示出范围来,然后根据在直线y-x=3的右下侧部分的面积,利用线性规划求出结果.
| OP |
| OA |
| OB |
解答:解:如图,过P作MN∥OB,则
=
+
=m
+n
=m
+n(
-
)
=m
+n(1+m)(
-
)
=-m
+n(1+m)
(m≥0,0≤n≤1)
所以
?
?
如图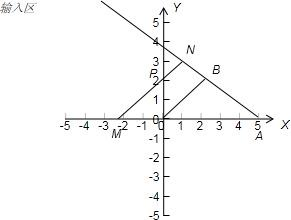
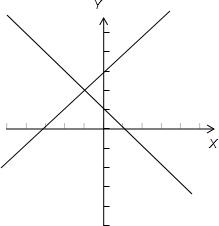
故选B
| OP |
| OM |
| MP |
| AO |
| MN |
| AO |
| AN |
| AM |
=m
| AO |
| AB |
| AO |
=-m
| OA |
| OB |
所以
|
|
|
如图


故选B
点评:本题考查二元一次不等式组与平面区域的关系,考查转化思想,是难题.

练习册系列答案
相关题目
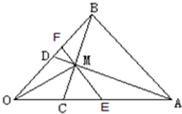 如图,在△OAB中,
如图,在△OAB中, (2013•杭州二模)如图,在△OAB中,C为OA上的一点,且
(2013•杭州二模)如图,在△OAB中,C为OA上的一点,且 如图,在△OAB中,已知
如图,在△OAB中,已知 如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=
如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=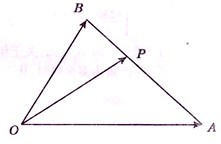 如图,在△OAB中,已知P为线段AB上的一点,且|
如图,在△OAB中,已知P为线段AB上的一点,且|