题目内容
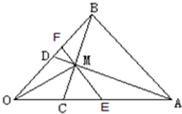 如图,在△OAB中,
如图,在△OAB中,| OC |
| 1 |
| 3 |
| OA |
| OD |
| 1 |
| 2 |
| OB |
设
| OA |
| a |
| OB |
| b |
(1)试用向量
| a |
| b |
| OM |
(2)在线段AC上取一点E,线段BD上取一点F,使EF过M点,
| OE |
| OA |
| OF |
| OB |
| 1 |
| λ |
| 2 |
| μ |
分析:由A,M,D三点共线可得存在实数t使得
=t
+(1-t)
=t
+(1-t)•
=
+t
同理由C,M,B三点共线可得存在实数λ使得
=λ
+(1-λ)
=λ
+
,根据向量的基本定理可建立关于t,λ的方程,求解即可
(2)设
=x
+y
=xλ
+yμ
由(1)可得
,从而可求
| OM |
| OA |
| OD |
| a |
| 1 |
| 2 |
| b |
| 1-t |
| 2 |
| b |
| a |
同理由C,M,B三点共线可得存在实数λ使得
| OM |
| OB |
| OC |
| b |
| 1-λ |
| 3 |
| a |
(2)设
| OM |
| OE |
| OF |
| a |
| b |
|
解答:解:(1)∵
=
,
=
由A,M,D三点共线可得存在实数t使得
=t
+(1-t)
=t
+(1-t)•
=
+t
同理由C,M,B三点共线可得存在实数λ使得
=λ
+(1-λ)
=λ
+
∴
∴λ=
,t=
∴
=
+
(2)设
=x
+y
=xλ
+yμ
?
?
+
=5
| OA |
| a |
| OB |
| b |
由A,M,D三点共线可得存在实数t使得
| OM |
| OA |
| OD |
| a |
| 1 |
| 2 |
| b |
| 1-t |
| 2 |
| b |
| a |
同理由C,M,B三点共线可得存在实数λ使得
| OM |
| OB |
| OC |
| b |
| 1-λ |
| 3 |
| a |
∴
|
| 2 |
| 5 |
| 1 |
| 5 |
∴
| OM |
| 1 |
| 5 |
| a |
| 2 |
| 5 |
| b |
(2)设
| OM |
| OE |
| OF |
| a |
| b |
|
|
| 1 |
| λ |
| 2 |
| μ |
点评:本题主要考查了平面向量的共线定理的应用:若A,B,C三点共线,O为直线外一点?存在实数λ,μ使得
=λ
+μ
,且λ+μ=1;还考查了向量的基本定理的应用.
| OC |
| OA |
| OB |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•杭州二模)如图,在△OAB中,C为OA上的一点,且
(2013•杭州二模)如图,在△OAB中,C为OA上的一点,且 如图,在△OAB中,已知
如图,在△OAB中,已知 如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=
如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=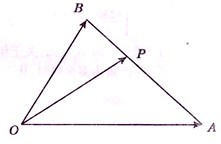 如图,在△OAB中,已知P为线段AB上的一点,且|
如图,在△OAB中,已知P为线段AB上的一点,且|