题目内容
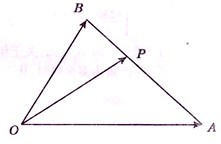 如图,在△OAB中,已知P为线段AB上的一点,且|
如图,在△OAB中,已知P为线段AB上的一点,且|| AP |
| PB |
(Ⅰ)试用
| OA |
| OB |
| OP |
(Ⅱ)若|
| OA |
| |OB| |
| OP |
| AB |
分析:(I)由题意,根据向量的三角形法则由
=2
,变形为关于
,
,
的方程,从中解出
的表达式即可;
(II)由(I)
=
+
,可将
•
用
,
数量积表示出来,再由|
|=3,
=2,且∠AOB=60°,计算出
•
的值
| AP |
| PB |
| OA |
| OB |
| OP |
| OP |
(II)由(I)
| OP |
| 1 |
| 3 |
| OA |
| 2 |
| 3 |
| OB |
| OP |
| AB |
| OB |
| OA |
| OA |
| |OB| |
| OP |
| AB |
解答:解:(I)∵P是线段AB上的一点,且|
|=2|
|.
∴
=2
.
即有
-
=2(
-
)
∴
=
+
(II)由(I)知
=
+
•
=(
+
)•(
-
)
=-
2-
•
+
2
=-
×9-
×3×2cos60°+
×4
=-
| AP |
| PB |
∴
| AP |
| PB |
即有
| OP |
| OA |
| OB |
| OP |
∴
| OP |
| 1 |
| 3 |
| OA |
| 2 |
| 3 |
| OB |
(II)由(I)知
| OP |
| 1 |
| 3 |
| OA |
| 2 |
| 3 |
| OB |
| OP |
| AB |
| 1 |
| 3 |
| OA |
| 2 |
| 3 |
| OB |
| OB |
| OA |
=-
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
| OA |
| 2 |
| 3 |
| OB |
=-
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
=-
| 4 |
| 3 |
点评:本题考点是向量在几何中的应用,综合考查了向量三角形法则,向量的线性运算,向量的数量积的运算及数量积公式,熟练掌握向量的相关公式是解题的关键,本题是向量基本题,计算题

练习册系列答案
相关题目
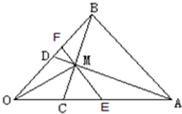 如图,在△OAB中,
如图,在△OAB中, (2013•杭州二模)如图,在△OAB中,C为OA上的一点,且
(2013•杭州二模)如图,在△OAB中,C为OA上的一点,且 如图,在△OAB中,已知
如图,在△OAB中,已知 如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=
如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=