题目内容
 如图,在△OAB中,已知|O
如图,在△OAB中,已知|O| A |
| B |
| 3 |
| D |
| B |
(1)若O
| C |
| P |
| D |
(2)记|P
| D |
分析:(1)以O为原点,OA为x轴,OB为y轴建立直角坐标系,记∠POB=α,由O
+O
=O
得
,从而可求
法1:(2)由
=(2-2λ-cosα,2
λ-sinα)可得f(λ)=
-1,结合二次函数的性质可求
法2:(2)|
|≥|
| -|
| =
-1|
|当且仅当P在线段OD上等号成立可得f(λ)=
-1下同法一
| C |
| P |
| D |
|
法1:(2)由
| PD |
| 3 |
| 16λ2-8λ+4 |
法2:(2)|
| PD |
| OD |
| OP |
| 16λ2-8λ+4 |
| PD |
| 16λ2-8λ+4 |
解答: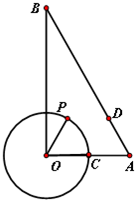 解:(1)以O为原点,OA为x轴,OB为y轴建立直角坐标系
解:(1)以O为原点,OA为x轴,OB为y轴建立直角坐标系
记∠POB=α则P(cosα,sinα),A(2,0),B(0,2
),C(1,0)
=
+λ
=(2(1-λ),2
λ)由OO
+O
=O
得
16λ2-4λ=0⇒λ=0或λ=
(5分)
(2)法1:
=(2-2λ-cosα,2
λ-sinα)
|
|2≥16λ2-8λ+5-
∴f(x)=
=
-1(4分)
∵16λ2-8λ+4=16(λ-
)2+3≥3
∴f(x)min=f(
)=
-1(2分)
法2:|
|≥|
| -|
| =
-1|
|当且仅当P在线段OD上等号成立
∴f(λ)=
-1(4分)
∵16λ2-8λ+4=16(λ-
)2+3≥3
∴f(x)min=f(
)=
-1(2分)
 解:(1)以O为原点,OA为x轴,OB为y轴建立直角坐标系
解:(1)以O为原点,OA为x轴,OB为y轴建立直角坐标系记∠POB=α则P(cosα,sinα),A(2,0),B(0,2
| 3 |
| OD |
| OA |
| AB |
| 3 |
| C |
| P |
| D |
得
|
| 1 |
| 4 |
(2)法1:
| PD |
| 3 |
|
| PD |
| 64λ2-32λ+16 |
∴f(x)=
16λ2-8λ+5-
|
| 16λ2-8λ+4 |
∵16λ2-8λ+4=16(λ-
| 1 |
| 4 |
∴f(x)min=f(
| 1 |
| 4 |
| 3 |
法2:|
| PD |
| OD |
| OP |
| 16λ2-8λ+4 |
| PD |
∴f(λ)=
| 16λ2-8λ+4 |
∵16λ2-8λ+4=16(λ-
| 1 |
| 4 |
∴f(x)min=f(
| 1 |
| 4 |
| 3 |
点评:本题主要考查了向量与三角函数的综合应用,向量的坐标表示及二次函数的最值的求解,属于综合试题

练习册系列答案
相关题目
 如图,在△OAB中,
如图,在△OAB中, (2013•杭州二模)如图,在△OAB中,C为OA上的一点,且
(2013•杭州二模)如图,在△OAB中,C为OA上的一点,且 如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=
如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB= 如图,在△OAB中,已知P为线段AB上的一点,且|
如图,在△OAB中,已知P为线段AB上的一点,且|