题目内容
在直角坐标系中,如果两点A(a,b),B(-a,-b)函数y=f(x)的图象上,那么称[A,B]为函数f(x)的一组关于原点的中心对称点([A,B]与[B,A]看作一组).函数g(x)=
关于原点的中心对称点的组数为______.
|
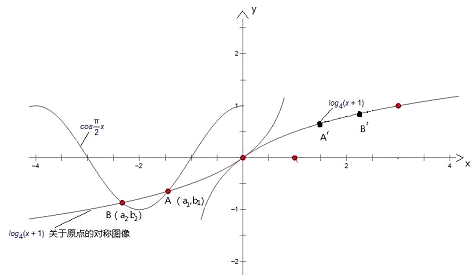
函数y=log4(x+1),x>0的图象过空心点(0,0)和实点(3,1),作出其关于原点的对称图象,如图,
显然它与函数y=cos
x,x≤0的图象有两个交点,因此关于原点的中心对称点的组数为2.
故答案为:2.
显然它与函数y=cos
| π |
| 2 |
故答案为:2.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的顶点坐标为
的顶点坐标为 ,且
,且 的两个实根之差等于
的两个实根之差等于 ,
, __________.
__________. 对任意的
对任意的 满足
满足 ,且当
,且当 时,
时, .若
.若 的取值范围是 .
的取值范围是 .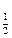 (a2-ax+2a)在[1,+∞
(a2-ax+2a)在[1,+∞ 上为减函数,则实数a的取值范围是( )
上为减函数,则实数a的取值范围是( )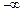 ,0)
,0)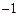 ,0)
,0)