题目内容
在平面直角坐标系xOy中，曲线y＝x2－6x＋1与坐标轴的交点都在圆C上．
(1)求圆C的方程；
(2)若圆C与直线x－y＋a＝0交于A，B两点，且OA⊥OB，求a的值．
(1)求圆C的方程；
(2)若圆C与直线x－y＋a＝0交于A，B两点，且OA⊥OB，求a的值．
（1）(x－3)2＋(y－1)2＝9.（2）a＝－1.
(1)曲线y＝x2－6x＋1与坐标轴的交点为(0,1)，(3±2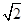
，0)．故可设圆心坐标为(3，t)，
则有32＋(t－1)2＝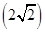
2＋t2.
解得t＝1，则圆的半径为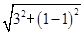
＝3.
所以圆的方程为(x－3)2＋(y－1)2＝9.
(2)设A(x1，y1)，B(x2，y2)，其坐标满足方程组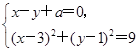
，
消去y得到方程2x2＋(2a－8)x＋a2－2a＋1＝0，
由已知可得判别式Δ＝56－16a－4a2＞0，
由根与系数的关系可得x1＋x2＝4－a，x1x2＝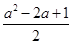
，①
由OA⊥OB可得x1x2＋y1y2＝0.又y1＝x1＋a，y2＝x2＋a.所以2x1x2＋a(x1＋x2)＋a2＝0.
由①②可得a＝－1，满足Δ＞0，故a＝－1.
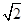，0)．故可设圆心坐标为(3，t)，则有32＋(t－1)2＝
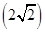2＋t2.解得t＝1，则圆的半径为
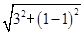＝3.所以圆的方程为(x－3)2＋(y－1)2＝9.
(2)设A(x1，y1)，B(x2，y2)，其坐标满足方程组
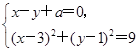，消去y得到方程2x2＋(2a－8)x＋a2－2a＋1＝0，
由已知可得判别式Δ＝56－16a－4a2＞0，
由根与系数的关系可得x1＋x2＝4－a，x1x2＝
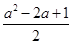，①由OA⊥OB可得x1x2＋y1y2＝0.又y1＝x1＋a，y2＝x2＋a.所以2x1x2＋a(x1＋x2)＋a2＝0.
由①②可得a＝－1，满足Δ＞0，故a＝－1.
练习册系列答案
相关题目
.
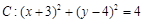过点
，且与圆
相切，求直线
的半径为4，圆心
：
上，且与圆
)作圆O:x2+y2=r2(r>0)的切线,切点为D,且|QD|=4.
=
+
,求|
＝0与圆C：x2＋y2＝4相交于A、B两点，
，若点M在圆C上，则实数k＝________.
被圆
所截得的弦长为________.
且与圆
相切的直线的方程是 .
与圆C：
交于
两点，则
的面积为（ ）
