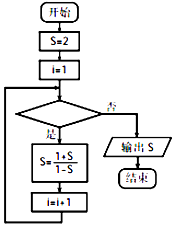
题目内容
【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60°.
(Ⅰ)证明:AB⊥A1C;
(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.
【答案】证明:(Ⅰ)取AB中点O,连接OC,OA1 , 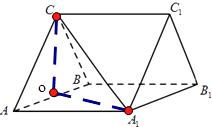
∵CA=CB,AB=A1A,∠BAA1=60°
∴OC⊥AB,OA1⊥AB,
∵OC∩OA1=O,
∴AB⊥平面OCA1 ,
∵CA1平面OCA1 ,
∴AB⊥A1C;
(Ⅱ)解:由(Ⅰ)知OC⊥AB,OA1⊥AB,又平面ABC⊥平面AA1B1B,交线为AB,
所以OC⊥平面AA1B1B,故OA,OA1 , OC两两垂直.
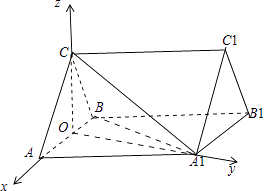
以O为坐标原点, ![]() 的方向为x轴的正向,建立如图所示的坐标系,
的方向为x轴的正向,建立如图所示的坐标系,
可得A(1,0,0),A1(0, ![]() ,0),C(0,0,
,0),C(0,0, ![]() ),B(﹣1,0,0),
),B(﹣1,0,0),
则 ![]() =(1,0,
=(1,0, ![]() ),
), ![]() =
= ![]() =(﹣1,
=(﹣1, ![]() ,0),
,0), ![]() =(0,﹣
=(0,﹣ ![]() ,
, ![]() ),
),
设 ![]() =(x,y,z)为平面BB1C1C的法向量,
=(x,y,z)为平面BB1C1C的法向量,
则 ![]() ,
,
可取y=1,可得 ![]() =(
=( ![]() ,1,﹣1),故cos<
,1,﹣1),故cos< ![]() ,
, ![]() >=﹣
>=﹣ ![]() ,
,
又因为直线与法向量的余弦值的绝对值等于直线与平面的正弦值,
故直线A1C与平面BB1C1C所成角的正弦值为: ![]() .
.
【解析】(Ⅰ)取AB中点,连接OC,OA1 , 得出OC⊥AB,OA1⊥AB,运用AB⊥平面OCA1 , 即可证明.(Ⅱ)易证OA,OA1 , OC两两垂直.以O为坐标原点, ![]() 的方向为x轴的正向建立坐标系,可向量的坐标,求出平面BB1C1C的法向量,代入向量夹角公式,可得答案.
的方向为x轴的正向建立坐标系,可向量的坐标,求出平面BB1C1C的法向量,代入向量夹角公式,可得答案.
【考点精析】关于本题考查的空间中直线直线之间的位置关系和空间角的异面直线所成的角,需要了解相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 才能得出正确答案.
才能得出正确答案.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案