题目内容
用数学归纳法证明1＋2＋3＋…＋(2n＋1)＝(n＋1)(2n＋1)时，从n＝k到n＝k＋1，左边需增添的代数式是( )
| A．2k＋2 | B．2k＋3 |
| C．2k＋1 | D．(2k＋2)＋(2k＋3) |
D
当n＝k时，左边是共有2k＋1个连续自然数相加，即
1＋2＋3＋…＋(2k＋1)，
所以当n＝k＋1时，左边是共有2k＋3个连续自然数相加，即
1＋2＋3＋…＋(2k＋1)＋(2k＋2)＋(2k＋3)，故选D.
1＋2＋3＋…＋(2k＋1)，
所以当n＝k＋1时，左边是共有2k＋3个连续自然数相加，即
1＋2＋3＋…＋(2k＋1)＋(2k＋2)＋(2k＋3)，故选D.
练习册系列答案
相关题目
≥8.
，
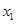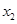是函数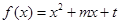
的两个零点，其中常数
，
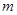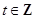，设
．
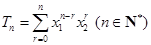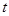表示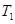
，
；
；
．
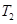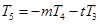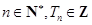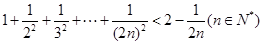，第二步证明“从
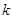到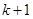
”，左端增加的项数是（ ）
＋
＋…＋
(
,
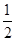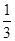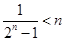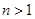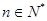)，在验证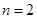
成立时，左式是____．
＋
＋…＋
>
的过程中，由n＝k推导n＝k＋1时，不等式的左边增加的式子是________．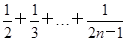
<n，其中n>1且n∈N*，在验证n＝2时，式子的左边等于________．