题目内容
(本小题满分10分)选修4—5;不等式选讲.
设不等式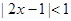 的解集是
的解集是 ,
, .
.
(I)试比较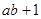 与
与 的大小;
的大小;
(II)设 表示数集
表示数集 的最大数.
的最大数. ,求证:
,求证: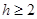 .
.
设不等式
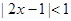 的解集是
的解集是 ,
, .
.(I)试比较
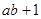 与
与 的大小;
的大小;(II)设
 表示数集
表示数集 的最大数.
的最大数. ,求证:
,求证: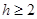 .
.(I)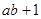 >
> ;
;
(II)见解析
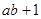 >
> ;
;(II)见解析
(1)先解出M={x|0<x<1}.
(I) 比较两个数的大小,最基本的方法就是作差比较.
即 .问题得证.
.问题得证.
(2) ,可知
,可知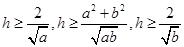 ,
,
所以根据不等式的性质,同向正向不等式具有可乘性,从而可证出 .
.
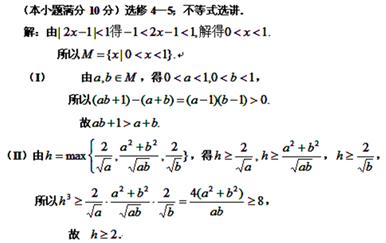
(I) 比较两个数的大小,最基本的方法就是作差比较.
即
 .问题得证.
.问题得证.(2)
 ,可知
,可知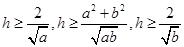 ,
,所以根据不等式的性质,同向正向不等式具有可乘性,从而可证出
 .
.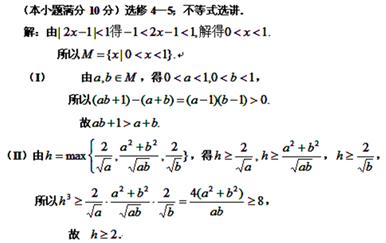

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
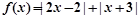 .
.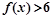 ;
; 的解集不是空集,试求
的解集不是空集,试求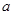 的取值范围.
的取值范围.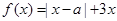 ,其中
,其中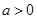 .
.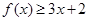 的解集.
的解集.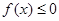 的解集为{x|
的解集为{x|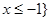 ,求a的值.
,求a的值.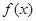 满足
满足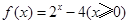 ,则不等式
,则不等式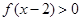 的解集是( )
的解集是( ) 
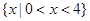

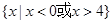
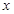 的不等式
的不等式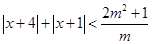 有解,则
有解,则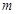 的取值范围为
的取值范围为  ,不等式
,不等式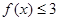 的解集为{x|-2
的解集为{x|-2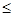
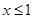 }。
}。 恒成立,求k的取值范围。
恒成立,求k的取值范围。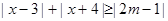 对于一切实数
对于一切实数 恒成立的实数
恒成立的实数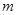 的取值范围为 .
的取值范围为 .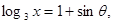 则
则 的值 .
的值 .