题目内容
设连续掷两次骰子得到的点数分别为m、n,令平面向量| a |
| b |
(Ⅰ)求使得事件“
| a |
| b |
(Ⅱ)求使得事件“|
| a |
| b |
(Ⅲ)使得事件“直线y=
| m |
| n |
分析:(I)利用乘法计数原理求出所有可能的取法,利用向量垂直的充要条件得到m-3n=0,通过列举法得到得事件“
⊥
”发生基本事件个数,利用古典概型的概率求出求出值.
(II)利用向量模的公式将事件|
|≤|
|”转化为m2+n2≤10,通过列举法得到该事件包含的基本事件个数,利用古典概型的概率求出求出值.
(III)由直线与圆的位置关系将事件“直线y=
x与圆(x-3)2+y2=1相交”转化为
<
,通过列举法得到该事件包含的基本事件个数,利用古典概型的概率求出求出值.
| a |
| b |
(II)利用向量模的公式将事件|
| a |
| b |
(III)由直线与圆的位置关系将事件“直线y=
| m |
| n |
| m |
| n |
| ||
| 4 |
解答:解:(I)由题意知,m∈{1,2,3,4,5,6};n∈{1,2,3,4,5,6},
故(m,n)所有可能的取法共6×6=36种(2分)
使得
⊥
,即m-3n=0,
即m=3n,共有2种(3,1)、(6,2),
所以求使得
⊥
的概率P=
=
(4分)
(Ⅱ)|
|≤|
|即m2+n2≤10,
共有(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)6种
使得|
|≤|
|的概率P=
=
(8分)
(Ⅲ)由直线与圆的位置关系得,d=
<1,
即
<
,
共有
,
,
,
,
,5种,
所以直线y=
x与圆(x-3)2+y2=1相交的概率P=
(12分)
故(m,n)所有可能的取法共6×6=36种(2分)
使得
| a |
| b |
即m=3n,共有2种(3,1)、(6,2),
所以求使得
| a |
| b |
| 2 |
| 36 |
| 1 |
| 18 |
(Ⅱ)|
| a |
| b |
共有(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)6种
使得|
| a |
| b |
| 6 |
| 36 |
| 1 |
| 6 |
(Ⅲ)由直线与圆的位置关系得,d=
| |3m| | ||
|
即
| m |
| n |
| ||
| 4 |
共有
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 2 |
| 6 |
所以直线y=
| m |
| n |
| 5 |
| 36 |
点评:求事件的概率,应该先判断出事件所属的概率模型,然后选择合适的概率公式,关键是求出基本事件的个数,常用的方法有:列举法、列表法、排列组合法、列树状图的方法.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
设连续掷两次骰子得到的点数分别为m、n,则直线y=
x与圆(x-3)2+y2=1相交的概率是( )
| m |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
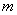 、
、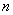 ,则直线
,则直线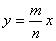 与圆
与圆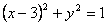 相交的概率是 ( )
相交的概率是 ( )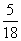 B.
B.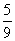 C.
C.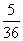 D.
D.